2022-2023年浙教版九年级（上）数学期中模拟试卷（杭州适用）

试卷更新日期：2022-10-14 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知2a=3b，则下列比例式不正确的是（）

A、 $\frac{3}{a}$ = $\frac{2}{b}$ B、 $\frac{a}{3}$ = $\frac{b}{2}$ C、 $\frac{b}{a}$ = $\frac{2}{3}$ D、 $\frac{2}{a}$ = $\frac{3}{b}$

查看试题解析
2. 台球盒中有7个红球与1个黑球，从中随机摸出一个台球，则下列描述符合的是（）

A、一定摸到黑球 B、不可能摸到黑球 C、很可能摸到黑球 D、不大可能摸到黑球

查看试题解析
3. 抛物线 $y = x^{2} - 2 x - 1$ 的图象向左平移2个单位，再向上平移3个单位，所得图象的解析式为（）

A、 $y = x^{2} - 6 x + 10$ B、 $y = x^{2} + 2 x + 2$ C、 $y = x^{2} - 6 x + 4$ D、 $y = x^{2} - 2 x - 4$

查看试题解析
4. 如图，两条直线被三条平行线所截，若AC＝4，CE＝6，BD＝2，则DF＝（）

A、1 B、2 C、3 D、4

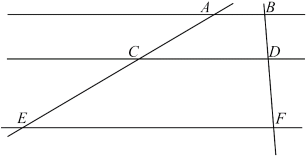查看试题解析
5. 如图，AB是 $⊙ O$ 的直径，点C在 $⊙ O$ 上，连接AC、BC，过点O作 $O D ∥ A C$ 交 $⊙ O$ 于点D，点C、D在AB的异侧．若 $∠ B = 24 °$ ，则 $∠ B C D$ 的度数是（）

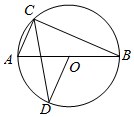A、66° B、67° C、57° D、48°

查看试题解析
6. 如图，在4×4的正方形网格中，若将△ABC绕着点A逆时针旋转得到△AB′C′，则 $\overset{⌢}{B B^{'}}$ 的长为（）

A、π B、 $\frac{π}{2}$ C、7 D、6

查看试题解析
7. 给出下列命题：①弦是直径；②半圆是弧；③长度相等的两段弧是等弧；④圆上两点间的线段叫弧；⑤过圆心的线段是直径；⑥直角三角形的三个顶点在同一个圆上.其中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 已知二次函数y＝ax²+bx+c（a＞0）的图象经过（0，1），（4，0），当该二次函数的自变量分别取x₁ ， x₂（0＜x₁＜x₂＜4）时，对应的函数值是y₁ ， y₂ ，且y₁＝y₂ ，设该函数图象的对称轴是直线x＝m，则m的取值范围是（）

A、0＜m＜1 B、1＜m≤2 C、2＜m＜4 D、0＜m＜4

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的y与x的部分对应值如表：
$x$
$- 1$
$0$
$1$
$3$
$y$
$- 3$
$1$
$3$
$1$
下列结论：①抛物线的开口向下；②其图象的对称轴为直线 $x = 1$ ；③当 $x < 2$ 时，函数值y随x的增大而增大；④方程 $a x^{2} + b x + c = 0$ 有一个根大于4．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，AB是半圆O的直径，AB＝5cm，AC＝4cm.D是弧BC上的一个动点（含端点B，不含端点C），连接AD，过点C作CE⊥AD于E，连接BE，在点D移动的过程中，BE的取值范围是（）

A、 $\sqrt{13} - 2 < B E \leq \frac{9}{5}$ B、 $\sqrt{13} - 2 \leq B E < 3$ C、 $\frac{9}{5} \leq B E < 3$ D、 $\sqrt{13} - \frac{9}{5} \leq B E < 3$

查看试题解析

二、填空题（每题4分，共24分）

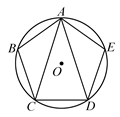
11. 已知线段a、b、c，其中c是a、b的比例中项，若a＝2cm，b＝8cm，则线段c＝cm.

查看试题解析
12. 不透明袋子中装有5个球，其中有2个红球、3个黑球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是黑球的概率是．

查看试题解析
13. 如图，⊙O是正五边形ABCDE的外接圆，则∠CAD=°.

查看试题解析
14. 如图，在每个小正方形的边长均为1的网格图中，一段圆弧经过格点 $A$ ， $B$ ， $C$ ，格点 $C$ ， $D$ 的连线交 $\overset{⌢}{B C}$ 于点 $E$ ，则 $\overset{⌢}{E C}$ 的长为．

查看试题解析
15. 已知二次函数 $y = x^{2} + (m - 3) x + m + 1$ ，当 $x > 1$ 时，y随x的增大而增大，则m的取值范围是．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ， $A C = 2$ ， $△ A B C$ 绕顶点 $C$ 逆时针旋转 $60 °$ 得到 $△ A^{'} B^{'} C$ ，点 $A$ 的对应点 $A^{'}$ 恰好落在 $A B$ 上，连接 $A^{'} B^{'}$ ，则图中阴影部分的面积为.

查看试题解析

三、解答题（共7题，共66分）

17. 我国新冠灭活疫苗主要来自三家生物制品公司，分别是A：科兴中维、B：北京所、C：武汉所．灭活疫苗一般需要接种2针，假如一人两次接种的疫苗的生产公司随机，请你用列表或树状图的方法求出一个人两次接种的疫苗刚好是同一家公司生产的概率．

查看试题解析
18. 如图，在△OAB 中，点 A 的坐标是（3，1），点 B 的坐标是（0，4），将△OAB 绕点 O 逆时针旋转 90°得到△OA₁B₁.

(1)、画出△OA₁B₁.

(2)、求点 B 旋转到点 B₁ 所经过的路径长（结果保留π）

查看试题解析
19. 如图，AB为⊙O的直径，C、D为圆上的两点，OC∥BD，OC交AD于点E．

(1)、求证：AC＝CD；

(2)、若OE＝2，AD＝8，求⊙O的半径．

查看试题解析
20. 某书店销售书刊，一天可售出20套，每套盈利40元。为了扩大销售，增加盈利，尽快减少库存，书店决定采取降价措施，若一套书每降价1元，平均每天可多售出2套。设每套书降价x元时，书店一天可获利y元。

(1)、求y关于x的函数表达式；

(2)、若书店每天盈利1200元，则需降价多少元？

(3)、当每套书降价多少元，书店可获最大利润？最大利润为多少？

查看试题解析
21. 如图，在等腰三角形ABC中，AB=AC，AD⊥BC，垂足为D．

(1)、请用尺规作图作出三角形ABC的外接圆⊙O；（不写作法及证明，应保留作图痕迹）

(2)、若BC＝4，AD=5，求⊙O的半径r．

查看试题解析
22. 已知二次函数y＝mx²﹣2mx+3，其中m≠0.

(1)、若二次函数的图象经过（1，4），求二次函数表达式；

(2)、若该二次函数图象开口向上，当﹣1≤x≤2时，二次函数图象的最高点为M，最低点为N，点M的纵坐标为6，求点M和点N的坐标；

(3)、在二次函数图象上任取两点（x₁ ， y₁），（x₂ ， y₂），当a≤x₁＜x₂≤a+2时，总有y₁＞y₂ ，求a的取值范围.

查看试题解析
23. 如图，AB为⊙O的直径，点C、D都在⊙O上，且CD平分∠ACB，交AB于点E.

(1)、求证：∠ABD＝∠BCD；

(2)、若DE＝13，AE＝17，求⊙O的半径；

(3)、DF⊥AC于点F，试探究线段AF、DF、BC之间的数量关系，并说明理由.

查看试题解析

$x$	$- 1$	$0$	$1$	$3$
$y$	$- 3$	$1$	$3$	$1$