河南省信阳九中2022-2023学年九年级上学期开学数学试卷
试卷更新日期:2022-10-12 类型:开学考试
一、选择题(本大题共10小题,共30分。)
-
1. 下列各数中,-2的绝对值是( )A、2 B、-2 C、 D、±22. 党的十八大以来,坚持把教育扶贫作为脱贫攻坚的优先任务. 年,中央财政累计投入“全面改善贫困地区义务教育薄弱学校基本办学条件”专项补助资金1692亿元,将169200000000用科学记数法表示应为( )A、 B、 C、 D、3. 已知442=1936,452=2025,462=2116,472=2209,若n为整数且n< <n+1,则n的值为( )A、44 B、45 C、46 D、474. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、 C、 D、5. 如图,在菱形中,对角线 , 相交于点 , 点是中点,连接 , 若 , , 则( )
 A、12 B、 C、6 D、6. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点将绕点顺时针旋转,每次旋转 , 则第2022次旋转结束时,点的坐标为( )
A、12 B、 C、6 D、6. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点将绕点顺时针旋转,每次旋转 , 则第2022次旋转结束时,点的坐标为( ) A、 B、 C、 D、7. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )
A、 B、 C、 D、7. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )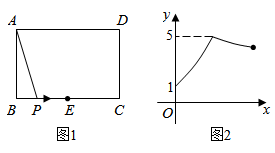 A、4 B、5 C、6 D、78. 如图,在四边形中, , , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 交于点若点是的中点,则的长为( )
A、4 B、5 C、6 D、78. 如图,在四边形中, , , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 交于点若点是的中点,则的长为( ) A、 B、4 C、3 D、9. 如果 , 那么的值为( )A、2或-1 B、0或2 C、2 D、-110. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( )
A、 B、4 C、3 D、9. 如果 , 那么的值为( )A、2或-1 B、0或2 C、2 D、-110. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共5小题,共15分)
-
11. 若 在实数范围内有意义,则实数 的取值范围是 .12. 有甲、乙两组数据,如下表所示:
甲
11
12
13
14
15
乙
12
12
13
14
05
甲、乙两组数据的方差分别为 , , 则填“”,“”或“” .
13. 方程的解是 .14. 如图1,点从的顶点出发,沿匀速运动到点 , 图2是点运动时,线段的长度随时间变化的关系图象,其中为曲线部分的最低点,则的面积是 .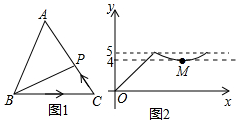 15. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
15. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
三、解答题(本大题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤)
-
16.(1)、计算;(2)、化简: .17. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.18. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.19. 2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
a.成绩频数分布表:
成绩x(分)
频数
7
9
12
16
6
b.成绩在 这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)、在这次测试中,成绩的中位数是分,成绩不低于80分的人数占测试人数的百分比为.(2)、这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.(3)、请对该校学生“航空航天知识”的掌握情况作出合理的评价.20. 如图,在 中, 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 .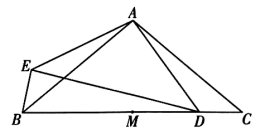 (1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.21. 近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的 倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.(1)、求菜苗基地每捆A种菜苗的价格.(2)、菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.22. 综合与实践
(1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.21. 近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的 倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.(1)、求菜苗基地每捆A种菜苗的价格.(2)、菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.22. 综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
 (1)、操作判断
(1)、操作判断操作一:对折矩形纸片 , 使与重合,得到折痕 , 把纸片展平;
操作二:在上选一点 , 沿折叠,使点落在矩形内部点处,把纸片展平,连接 , .
根据以上操作,当点在上时,写出图1中一个的角: .
(2)、迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片按照(1)中的方式操作,并延长交于点 , 连接 .
①如图2,当点在上时,_▲_ , _▲_;
②改变点在上的位置点不与点 , 重合 , 如图3,判断与的数量关系,并说明理由.
(3)、拓展应用在(2)的探究中,已知正方形纸片的边长为 , 当时,直接写出的长.
23. 如图,二次函数的图象经过点和点 , 点的坐标为 . (1)、求二次函数的解析式;(2)、若轴上有一点 , 点是抛物线上一动点,过点作轴于点 .
(1)、求二次函数的解析式;(2)、若轴上有一点 , 点是抛物线上一动点,过点作轴于点 .求证:点在线段的垂直平分线上;
若点 , 求的周长的最小值.