广西壮族自治区玉林市北流市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 下列新冠疫情防控标识图案中，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 在下列方程中，属于一元二次方程的是（）。

A、3x-4=0 B、x²-3x=0 C、x+3y=2 D、 $\frac{2}{x - 1}$ =3

查看试题解析
3. 对于二次函数 y＝（x－2）²＋2的图象，下列说法正确的是（）

A、开口向下 B、当x＝－2时，y有最大值是2 C、对称轴是x＝－2 D、顶点坐标是（2，2）

查看试题解析
4. 苹果熟了，从树上落下所经过的路线s与下落的时间t满足s= $\frac{1}{2} g t^{2}$ （g是不为0的常数），则s与t的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
5. 如图，将 $R t △ A B C$ （其中 $∠ B = 34 °$ ， $∠ C = 90 °$ ），绕 $A$ 点按顺时针方向旋转到 $△ A B_{1} C_{1}$ 的位置，使得点 $C$ ， $A$ ， $B_{1}$ 在同一直线上，则旋转角的度数为（）

A、56° B、68° C、124° D、180°

查看试题解析
6. 抛物线 $y = x^{2}, y = - 3 x^{2}, y = \frac{1}{2} x^{2}$ 的共同性质是（）

A、开口向上 B、都有最大值 C、对称轴都是x轴 D、顶点都是原点

查看试题解析
7. 关于x的一元二次方程 $x^{2} = 1$ 的根是（）

A、 $x = 1$ B、 $x_{1} = 1$ ， $x_{2} = - 1$ C、 $x = - 1$ D、 $x_{1} = x_{2} = 1$

查看试题解析
8. 若将抛物线 $y = 2 x^{2} + 3$ 向右平移3个单位，再向上平移2个单位，则所得抛物线的解析式为（）

A、 $y = 2 (x + 3)^{2} + 5$ B、 $y = 2 (x - 3)^{2} + 5$ C、 $y = 2 (x + 3)^{2} - 1$ D、 $y = 2 (x - 3)^{2} - 1$

查看试题解析
9. 已知关于x的一元二次方程 $x^{2} + 2 m = 4 x$ 有两个实数根，则m的取值范围是（）

A、m≤2 B、m＜2 C、m≥0 D、m＜0

查看试题解析
10. 一个长方形的长比宽多2，若把它的长、宽分别增加2后，面积增加了24，求原来长方形的长与宽，若设原长方形的宽为x，可列方程为（）

A、x（x＋2）＝24 B、（x＋4）（x＋2）＝24 C、（x＋4）（x＋2）－x（x＋2）＝24 D、x（x＋4）＝24

查看试题解析
11. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的位置如图所示，则关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有两个实数根 D、没有实数根

查看试题解析
12. 如图，在菱形OABC中，点A在x轴上，B（4，2），将菱形OABC绕原点O逆时针旋转90°，若点C的对应点是点 $C_{1}$ ，那么点 $C_{1}$ 坐标是（）

A、（-2，4） B、（-2.5，2） C、（-1.5，2） D、（-2，1.5）

查看试题解析

二、填空题

13. 抛物线 $y = - \frac{1}{2} x^{2}$ 的开口向（填“上”或“下”）．

查看试题解析
14. 若点（2，y₁）和点（4，y₂）在函数y＝x²的图象上，则y₁y₂（填“＞”、“＜”或“＝”）．

查看试题解析
15. 设 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - m x + m - 1 = 0$ 的两个根．若 $x_{1} + x_{2} = 3$ ，则 $x_{1} x_{2} =$ ．

查看试题解析
16. 如图，在平面直角坐标系中，△ABC绕旋转中心顺时针旋转90°后得到△A'B'C'，则其旋转中心的坐标是.

查看试题解析
17. 某飞机着陆后靠惯性滑行的路程 $s$ 米与时间 $t$ 秒满足关系式 $s = 200 t - \frac{5}{3} t^{2}$ ，那么该飞机着陆后滑行到停止的时间为秒.

查看试题解析
18. 如图，已知二次函数 $y = a x^{2} + b x + c$ （a≠0（的图象，且关于x的一元二次方程 $a x^{2} + b x + c - m = 0$ 没有实数根，有下列结论：① $b^{2} - 4 a c > 0$ ；② $a b c < 0$ ；③ $m < - 3$ ；④ $3 a + b > 0$ .其中正确结论的序号有.

查看试题解析

三、解答题

19. 解方程：x²+2x﹣3＝0．

查看试题解析
20. 已知抛物线经过点A（－3，0）、B（1，0）、C（0，3），求抛物线的解析式．

查看试题解析
21. 正方形网格中（每个小正方形边长是1，小正方形的顶点叫做格点）， $Δ A B C$ 的顶点均在格点上，请在所给的平面直角坐标系中解答下列问题：

(1)、作出 $Δ A B C$ 绕点 $A$ 逆时针旋转90°后的 $Δ A_{1} B_{1} C_{1}$ ；

(2)、作出 $Δ A_{1} B_{1} C_{1}$ 关于原点 $O$ 成中心对称的 $Δ A_{2} B_{2} C_{2}$ .

查看试题解析
22. 已知关于x的方程x²﹣2x+m=0有两个不相等的实数根x₁、x₂

(1)、求实数m的取值范围；

(2)、若x₁﹣x₂=2，求实数m的值．

查看试题解析
23. 如图， $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $A C = 8 c m$ ， $B C = 4 c m$ ，一动点P从点C出发沿着 $C B$ 方向以 $1 c m / s$ 的速度运动，另一动点Q从A出发沿着 $A C$ 边以 $2 c m / s$ 的速度运动，P，Q两点同时出发，运动时间为 $t (s)$ .

(1)、若 $△ P C Q$ 的面积是 $△ A B C$ 面积的 $\frac{1}{4}$ ，求t的值？

(2)、△PCQ的面积能否为 $△ A B C$ 面积的一半？若能，求出t的值；若不能，说明理由.

查看试题解析
24. 如图，△ABC中，点E在BC边上.AE=AB，将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF，EF与AC交于点G.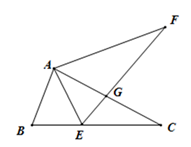

(1)、求证：EF =BC；

(2)、若∠ABC=65°，∠ACB=28°，求∠FGC的度数.

查看试题解析
25. 新冠肺炎疫情期间，某药店进了一批口罩，每包进价10元，每包销售价定为25元时，每天销售1000包．经一段时间调查，发现每包销售单价每上涨1元，每天就少卖40包．其销售单价不低于进价，销售利润率不高于180% ．设每包销售价为x元（x为正整数）．

(1)、请直接写出 $x$ 的取值范围．

(2)、设每天的总利润为 $w$ 元，当每包销售价定为多少元时，该药店每天的利润最大？最大利润是多少元？

查看试题解析
26. 如图1，抛物线y＝﹣ $\frac{1}{2}$ x²＋bx＋c与x轴交于点A（﹣1，0）和点B（3，0）．P为该抛物线上一动点，设点P的横坐标为m．

(1)、求抛物线的解析式．

(2)、将该抛物线沿y轴向下平移 $\frac{1}{2}$ AB个单位长度，点P的对应点为P′，若OP＝OP′，求△OPP′的面积．

(3)、如图2，连接AP，BP，设△APB的面积为S，当－2≤m≤2时，求S的最大值．

查看试题解析