广西壮族自治区南宁市横县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 把一元二次方程（x-3）²＝5化为一般形式后，二次项系数为（）

A、1 B、2 C、3 D、5

查看试题解析
2. 下列现象中属于旋转的是（）

A、汽车在急刹车时向前滑动 B、拧开水龙头 C、雪橇在雪地里滑动 D、电梯的上升与下降

查看试题解析
3. 下列，图形中，是轴对称而不是中心对称图形是（）

A、等边三角形 B、矩形 C、平行四边形 D、菱形

查看试题解析
4. 抛物线y＝x²+1的对称轴是（）

A、直线x＝﹣1 B、直线x＝1 C、直线x＝0 D、直线y＝1

查看试题解析
5. 一元二次方程 $x^{2} - 2 x - 1 = 0$ 的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 如图，这是二次函数y＝x²﹣2x﹣3的图象，根据图象可知，函数值小于0时x的取值范围为（）

A、x＜-1 B、x＜3 C、-1＜x＜3 D、x >3

查看试题解析
7. 如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为（）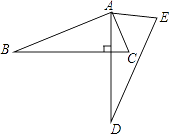

A、60° B、75° C、85° D、90°

查看试题解析
8. 用配方法解方程 $x^{2} - \frac{2}{3} x - 1 = 0$ 应该先变形为（）

A、 $(x - \frac{1}{3})^{2} = \frac{8}{9}$ B、 $(x - \frac{1}{3})^{2} = - \frac{8}{9}$ C、 $(x - \frac{1}{3})^{2} = \frac{10}{9}$ D、 $(x - \frac{2}{3})^{2} = 0$

查看试题解析
9. 如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是（）

A、72° B、108° C、144° D、216°

查看试题解析
10. 如图，在一幅长 $60 c m$ ，宽 $40 c m$ 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是 $2816 c m^{2}$ ，设金色纸边的宽为 $x c m$ ，那么x满足的方程是（）

A、 $(60 + x) (40 + 2 x) = 2816$ B、 $(60 + x) (40 + x) = 2816$ C、 $(60 + 2 x) (40 + x) = 2816$ D、 $(60 + 2 x) (40 + 2 x) = 2816$

查看试题解析
11. 二次函数 $y$ = $a$ $x^{2}$ +4 $x$ + $a$ 的最大值为3，则 $a$ 的值为（）

A、－4 B、－1 C、1 D、4

查看试题解析
12. 如图，抛物线 $y = x^{2} - 2 x - 3$ 与 $y$ 轴交于点C，点D的坐标为（0，－1），在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，则点P的横坐标为（）

A、1＋ $\sqrt{2}$ B、1－ $\sqrt{2}$ C、 $\sqrt{2}$ －1 D、1－ $\sqrt{2}$ 或1＋ $\sqrt{2}$

查看试题解析

二、填空题

13. 若 $y = x^{m - 1} + 2 x$ 是关于 $x$ 的二次函数，则m＝

查看试题解析
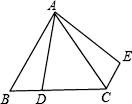
14. 已知方程x²－3x＋m＝0的一个根是1，m的值是．

查看试题解析
15. 平面直角坐标系内点M（－3，3）关于原点对称的点的坐标是．

查看试题解析
16. 如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为．

查看试题解析
17. 方程（a－1）x²＋2（a＋1）x＋a＋5=0有两个实根，则正整数a的值为.

查看试题解析
18. 如图，已知抛物线 $y = x^{2}$ +P $x$ +q的对称轴为直线 $x$ =－2，过其顶点 $M$ 的一条直线 $y = k x + b$ 与该抛物线的另一个交点为 $N$ （－1，－1）．若在 $y$ 轴上存在一点P，使得PM+PN最小，则点P的坐标为.

查看试题解析

三、解答题

19. 解方程：4 $x^{2}$ =81

查看试题解析
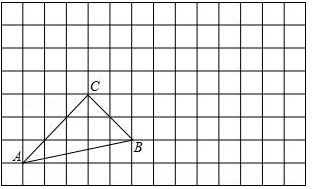
20. 解方程 $x^{2} - 4 x - 7 = 0$

查看试题解析
21. 在网格图中，作出△ABC绕点B顺时针方向旋转90°得到的△A′B′C′．

查看试题解析
22. 如图是二次函数 $y$ = $\frac{1}{2} x^{2}$ －6 $x$ +21的图象，请回答以下问题：

(1)、写出抛物线的顶点坐标和对称轴；

(2)、当 $x$ 取什么值时， $y$ 随 $x$ 的增大而增大？

(3)、当x取什么值时， $y$ 随 $x$ 的增大而减小？

查看试题解析
23. 已知一直角三角形两条直角边的和等于8，若其中一直角边为 $x$ .

(1)、写出这个直角三角形的面积 $S$ 关于 $x$ 的函数解析式；

(2)、当两条直角边各为多少时这个直角三角形的面积最大？

查看试题解析
24. 某工厂为了提高市场竞争力不断改进设备，2018年在改进设备方面投入的资金是100万元，2020年投入的资金是121万元，且从2018年到2020年每年投入资金的年平均增长率相同.

(1)、求该工厂在改进设备方面投入资金的年平均增长率；

(2)、若投入资金的年平均增长率不变，那么该厂在2021年需投入多少万元？

查看试题解析
25. 【探索发现】如图①，四边形ABCD是正方形，M，N分别在边CD、BC上，且∠MAN=45°，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．如，小明将△ADM绕点A顺时针旋转90°，点D与点B重合，得到△ABE，如图②．从而证明出了DM+BN=MN．

(1)、请你按照小明的方法证明：DM+BN=MN；

(2)、【类比延伸】
如图③，点N、M分别在正方形ABCD的边BC、CD的延长线上，∠MAN=45°，连接数MN，请根据小明的发现给你的启示写出MN、DM、BN之间的数量关系，并证明．

查看试题解析
26. 如图，在坐标系中△ABC是等腰直角三角形，∠BAC =90°，A（1， 0），B（0， 2），抛物线 $y = \frac{1}{2} x^{2} - b x - 2$ 的图象过点（2，-1）及点C.

(1)、求该抛物线的解析式；

(2)、求点C的坐标

(3)、点P是抛物线上一动点，是否存在点P，使以P，A，C，B为顶点的四边形是平行四边形？若存在，求出P点坐标；若不存在，说明理由.

查看试题解析