广西壮族自治区柳州市三江侗族自治县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程的解是( )A、 B、 C、 D、3. 抛物线y=ax2+bx+c(a≠0)过(2,8)和(﹣6,8)两点,则此抛物线的对称轴为( )A、直线x=0 B、直线x=1 C、直线x=﹣2 D、直线x=﹣14. 下列方程中是一元二次方程的是( )A、y+2=1 B、=0 C、 D、5. 已知关于的方程的一个根为 , 则实数的值为A、1 B、﹣1 C、2 D、﹣26. 如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( )
2. 一元二次方程的解是( )A、 B、 C、 D、3. 抛物线y=ax2+bx+c(a≠0)过(2,8)和(﹣6,8)两点,则此抛物线的对称轴为( )A、直线x=0 B、直线x=1 C、直线x=﹣2 D、直线x=﹣14. 下列方程中是一元二次方程的是( )A、y+2=1 B、=0 C、 D、5. 已知关于的方程的一个根为 , 则实数的值为A、1 B、﹣1 C、2 D、﹣26. 如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( )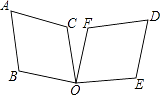 A、∠BOF B、∠AOD C、∠COE D、∠COF7. 若关于x的一元二次方程3x2+k=0有实数根,则( )A、k>0 B、k<0 C、k≥0 D、k≤08. 二次函数y=x2﹣x﹣2的图象如图所示,则函数值y<0时x的取值范围是( )
A、∠BOF B、∠AOD C、∠COE D、∠COF7. 若关于x的一元二次方程3x2+k=0有实数根,则( )A、k>0 B、k<0 C、k≥0 D、k≤08. 二次函数y=x2﹣x﹣2的图象如图所示,则函数值y<0时x的取值范围是( ) A、x<﹣1 B、x>2 C、﹣1<x<2 D、x<﹣1或x>29. 将抛物线 向上平移1个单位,再向右平移2个单位,则平移后的抛物线为( )A、 B、 C、 D、10. 某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为 ,则可列方程为( )A、 B、 C、 D、11. 若A(-6,y1),B(-3,y2),C(1,y3)为二次函数图象上的三点,则y1 , y2 , y3的大小关系是( )A、y2<y3<y1 B、y1<y2<y3 C、y3<y1<y2 D、y2<y1<y312. 如图,三个顶点的坐标分别为 , , , 将绕点按顺时针方向旋转 , 得到 , 则点的坐标为( )
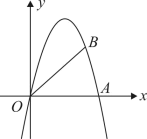
A、x<﹣1 B、x>2 C、﹣1<x<2 D、x<﹣1或x>29. 将抛物线 向上平移1个单位,再向右平移2个单位,则平移后的抛物线为( )A、 B、 C、 D、10. 某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为 ,则可列方程为( )A、 B、 C、 D、11. 若A(-6,y1),B(-3,y2),C(1,y3)为二次函数图象上的三点,则y1 , y2 , y3的大小关系是( )A、y2<y3<y1 B、y1<y2<y3 C、y3<y1<y2 D、y2<y1<y312. 如图,三个顶点的坐标分别为 , , , 将绕点按顺时针方向旋转 , 得到 , 则点的坐标为( ) A、(1, 2) B、(2, 1) C、(1, 1) D、(2, 2)
A、(1, 2) B、(2, 1) C、(1, 1) D、(2, 2)二、填空题
-
13. 抛物线的对称轴是直线 .14. 点(-2,5)关于原点对称的点的坐标是 .15. 如图,ABC绕点A旋转后到达ADE处,若∠BAC=120°,∠BAD=30°,则∠CAE=
 16. 抛物线的顶点坐标是 .17. 二次函数的图象如图所示,则一次函数的图象不经过 .
16. 抛物线的顶点坐标是 .17. 二次函数的图象如图所示,则一次函数的图象不经过 . 18. 已知代数式 的值是7,则代数式 的值是 .
18. 已知代数式 的值是7,则代数式 的值是 .三、解答题
-
19. 解方程:(1)、x(x -2)+ x -2 = 0(2)、x2 - 4x + 1 = 0 (用配方法)20. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC 的顶点均在格点上,点A的坐标为(1,-4).

(1)△A1B1C1是△ABC关于y轴的对称图形,则点A的对称点A1的坐标是 , 并在图中画出△A1B1C1 .
(2)将△ABC绕原点逆时针旋转90°得到△A2B2C2 , 则A点的对应点A2的坐标是 , 并在图中画出△A2B2C2 .21. 已知二次函数图象的顶点坐标为M(1,﹣2),且经过点N(2,3),求这个二次函数的解析式.22. 如图所示,在一块长为米,宽为米的矩形草地上,在中间要设计-横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?