广西壮族自治区柳州市柳江区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、x+y﹣1=0 B、x﹣﹣2=0 C、x2=x+1 D、x+1=2x2. 下列函数是二次函数的是( )A、y=ax2+bx+c B、y=2x﹣1 C、y=2x2﹣3x+1 D、y=2x2﹣3x33. 下列四个银行标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
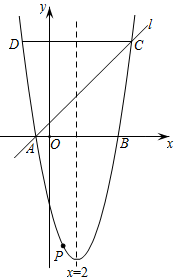
D、 4. 如图,将正方形ABCD绕点D逆时针方向旋转180°后,点B的坐标是( )
4. 如图,将正方形ABCD绕点D逆时针方向旋转180°后,点B的坐标是( ) A、(0,2) B、(0,﹣3) C、(2,﹣1) D、(2,1)5. 方程x2﹣3x=0的根为( )A、0 B、3 C、0或3 D、0或6. 用配方法解方程 , 方程应变形为( )A、 B、 C、 D、7. 一元二次方程的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=35°,则∠BDC=( )
A、(0,2) B、(0,﹣3) C、(2,﹣1) D、(2,1)5. 方程x2﹣3x=0的根为( )A、0 B、3 C、0或3 D、0或6. 用配方法解方程 , 方程应变形为( )A、 B、 C、 D、7. 一元二次方程的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=35°,则∠BDC=( ) A、85° B、75° C、70° D、55°9. 将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x+1)2+2,下列平移方式中,正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向上平移2个单位 D、先向右平移1个单位,再向下平移2个单位10. 已知抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),则代数式m2﹣2m+2021的值为( )A、2020 B、2021 C、2022 D、202311. 如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若 , 则( )
A、85° B、75° C、70° D、55°9. 将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x+1)2+2,下列平移方式中,正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向上平移2个单位 D、先向右平移1个单位,再向下平移2个单位10. 已知抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),则代数式m2﹣2m+2021的值为( )A、2020 B、2021 C、2022 D、202311. 如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若 , 则( ) A、2 B、3 C、4 D、512. 如图所示的是二次函数y=ax2+bx+c的图象,下面五条信息中:(1)a<0;(2)b2﹣4ac>0;(3)c>1;(4)2a﹣b>0;(5)a+b+c<0.其中错误信息的个数是( )
A、2 B、3 C、4 D、512. 如图所示的是二次函数y=ax2+bx+c的图象,下面五条信息中:(1)a<0;(2)b2﹣4ac>0;(3)c>1;(4)2a﹣b>0;(5)a+b+c<0.其中错误信息的个数是( )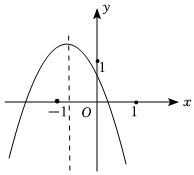 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
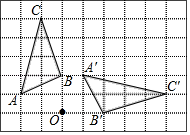
13. 抛物线y=3(x﹣5)2+2的顶点坐标是 .14. 若3是方程x2﹣x﹣b=0的一个根,则b的值为 .15. 在今年举办的东京奥运会上,杨倩在女子10米气步枪决赛中夺得冠军,为中国代表团揽入首枚金牌,随后杨倩同款“小黄鸭”发卡在电商平台上爆单,该款发卡在某电商平台上月24日的销量为5000个,7月25日和7月26日的总销量是22500个.若7月25日和26日较前一天的增长率均为x,则x满足的方程是 .16. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 . .
 17. 往水平放置的半径为10cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=16cm,则水的最大深度为 .
17. 往水平放置的半径为10cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=16cm,则水的最大深度为 .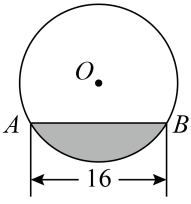 18. 如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为 .
18. 如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为 .
三、解答题
-
19. 解方程:x2+2x﹣3=0.20. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,已知A(1,3),B(4,5),C(5,1).
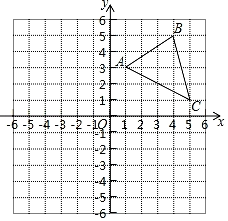
(1)作出△A1B1C1 , 使它和△ABC关于y轴对称;
(2)作出△A2B2C2 , 使它和△ABC关于原点O对称,点A,B,C的对应点分别为A2 , B2 , C2;
(3)直接写出点A2 , B2的坐标.21. 如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D. (1)、求证AC=BD;(2)、若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是 .22. 某种病毒传播非常快,如果一个人被感染,经过两轮感染后就会有121个人被感染.(1)、每轮感染中平均一个人会感染几个人?(2)、若病毒得不到有效控制,3轮感染后,被感染的人会不会超过1300人?23. 正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)、求证AC=BD;(2)、若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是 .22. 某种病毒传播非常快,如果一个人被感染,经过两轮感染后就会有121个人被感染.(1)、每轮感染中平均一个人会感染几个人?(2)、若病毒得不到有效控制,3轮感染后,被感染的人会不会超过1300人?23. 正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.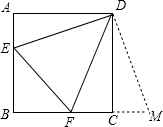 (1)、求证:EF=FM(2)、当AE=1时,求EF的长.24. 2021端午节前夕,某商铺推出了肉粽和蜜枣粽两种精美礼盒,其中肉粽礼盒的单价为180元/盒,蜜枣粽礼盒的单价为120元/盒.(1)、5月份,销售了肉粽和蜜枣粽礼盒共200盒,销售总额为26400元,问5月份销售了多少盒肉粽礼盒?(2)、6月份,商铺决定调整营销方案,将肉粽礼盒的单价在原有基础上下调m元,蜜枣粽礼盒的单价不变,这样肉粽礼盒的销量较5月份肉粽礼盒的销量涨了10m盒,蜜枣粽礼盒的销售较5月份蜜枣粽礼盒的销量减少了10m盒,且6月份肉粽礼盒的销量不超过6月份蜜枣粽礼盒的销量,设6月份的销售总额为w元,问当m为何值时,销售总额最大,最大为多少元?
(1)、求证:EF=FM(2)、当AE=1时,求EF的长.24. 2021端午节前夕,某商铺推出了肉粽和蜜枣粽两种精美礼盒,其中肉粽礼盒的单价为180元/盒,蜜枣粽礼盒的单价为120元/盒.(1)、5月份,销售了肉粽和蜜枣粽礼盒共200盒,销售总额为26400元,问5月份销售了多少盒肉粽礼盒?(2)、6月份,商铺决定调整营销方案,将肉粽礼盒的单价在原有基础上下调m元,蜜枣粽礼盒的单价不变,这样肉粽礼盒的销量较5月份肉粽礼盒的销量涨了10m盒,蜜枣粽礼盒的销售较5月份蜜枣粽礼盒的销量减少了10m盒,且6月份肉粽礼盒的销量不超过6月份蜜枣粽礼盒的销量,设6月份的销售总额为w元,问当m为何值时,销售总额最大,最大为多少元?