广西壮族自治区贺州市平桂区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数表达式中，是二次函数的是（）．

A、 $y = \frac{1}{x}$ B、y=x+2 C、y=x²+1 D、y=（x+3）²-x²

查看试题解析
2. 已知C是线段AB的中点，则 $\frac{B C}{A B}$ 的值为（）．

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
3. 下列函数是反比例函数的是（）．

A、 $y = - \frac{1}{x}$ B、y=-2x C、y=-2 x+1 D、y=x²-x

查看试题解析
4. 对于抛物线y=-x² ，下列说法不正确的是（）．

A、开口向下 B、对称轴为直线x=0 C、顶点坐标为（0，0） D、y随x的增大而减小

查看试题解析
5. 关于反比例函数 $y = \frac{3}{x}$ 的图象，下列说法正确的是（）．

A、图象经过点（1，2） B、图象位于第一、三象限内 C、图象位于第二、四象限内 D、y随x的增大而减小

查看试题解析
6. 抛物线 $y = - (x + 1)^{2} - 4$ 的顶点坐标为（）．

A、（-1，-4） B、（-1，4） C、（1，-4） D、（1，4）

查看试题解析
7. 下列四条线段中，成比例的是（）．

A、a=1，b=2，c=3，d=4 B、a=1，b=2，c=3，d=6 C、a=2，b=3，c=4，d=7 D、a=3，b=2，c=5，d=4

查看试题解析

8. 下列表格是二次函数

y = a x^{2} + b x + c

的自变量x与函数值y的对应值，判断方程

a x^{2} + b x + c = 1

（a≠0，a，b，c，为常数）的一个解x的范围是（）．

x	6.17	6.18	6.19	6.20	6.21
y=ax²+bx+c	-0.3	0.1	0.6	1.2	2.0

A、6.17<x<6.18 B、6.18<x<6.19 C、6.19<x<6.20 D、6.20<x<6.21

查看试题解析

9. 已知抛物线 $y = x^{2} - （ m - 1) x + 4$ 的顶点在x轴上，则m的值为（）．

A、-3 B、0 C、5 D、-3或5

查看试题解析
10. 如图，点A的坐标是（4，0），△ABO是等边三角形，点B在第一象限．若反比例函数 $y = \frac{k}{x}$ （x>0）的图象经过点B，则k的值是（）．

A、4 B、8 C、4 $\sqrt{3}$ D、 $8 \sqrt{3}$

查看试题解析
11. 如图，抛物线y＝ax²＋bx＋c交x轴于（-1，0），（3，0），则下列判断错误的是（）．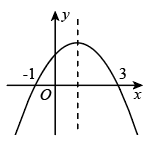

A、图象的对称轴是直线x＝1 B、当x>1时，y随x的增大而减小 C、一元二次方程ax²＋bx＋c＝0的两个根分别是-1和3 D、当y<0时，x<-1

查看试题解析
12. 如图，二次函数y＝ax²＋bx＋c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，点B的坐标为（1，0），下面的四个结论：① abc>0；② a-b＋c<0；③ 2a-b=0；④3a+c>0．其中正确结论个数有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 长方体的长和宽都为x，高为10，它的体积y与高x的函数关系式为．（不要求写出自变量取值范围）．

查看试题解析
14. 反比例函数 $y = \frac{k}{x}$ 的图象在二、四象限，则k的值为．（写出一个即可）

查看试题解析
15. 若 $\frac{a}{b} = \frac{3}{5}$ ，则 $\frac{a + b}{b}$ ＝.

查看试题解析
16. 已知点A（-1， $y_{1}$ ），B（-3， $y_{2}$ ）在二次函数 $y = (x - 1)^{2} + k$ 的图象上，则 $y_{1}$ $y_{2}$ ．（填“>”“<”或“=”）．

查看试题解析
17. 若函数 $y = x^{2} - 3 x + c$ 的图象与坐标轴有三个交点，则c的取值范围是．

查看试题解析
18. 在平面直角坐标系中，将抛物线 $y = x^{2} - b x + c$ 向下平移1个单位，再向左平移1个单位后顶点与原点重合，则不等式 $\frac{2 b}{x} < b x + c$ 的解集是．

查看试题解析

三、解答题

19. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（-2，3），求该反比例函数的表达式．

查看试题解析
20. 已知a∶b=1∶3，且2a+b=10，求a的值．

查看试题解析
21. 某养鱼专业户准备挖一个面积为2600平方米的矩形鱼塘．

(1)、写出鱼塘的长y（米）关于宽x（米）的函数表达式；（不要求写出自变量的取值范围）

(2)、由于受场地的限制，鱼塘的宽最多只能挖40米，当鱼塘的宽是40米时，鱼塘的长是多少米?

查看试题解析
22. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，根据图象解答下列问题

(1)、写出方程 $a x^{2} + b x + c = 0$ 的两个根；

(2)、写出不等式 $a x^{2} + b x + c > 0$ 的解集

查看试题解析
23. 二次函数图象的对称轴是y轴，最大值为4，且过点A（1，2），与x轴交于B、C两点．求△ABC的面积．

查看试题解析
24. 杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线y= $- \frac{3}{5}$ x²+3x+1的一部分，如图所示．

(1)、求演员弹跳离地面的最大高度；

(2)、已知人梯高BC=3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．

查看试题解析
25. 如图，在△ABC中，∠ADE=∠B=∠EFC，AD∶BD=5∶3，CF=9．

(1)、求证：四边形BDEF是平行四边形；

(2)、求DE的长

查看试题解析
26. 已知，抛物线 $y = a x^{2} + b x - 5$ 与x轴交于点A（5，0），且过点（1，-8）．

(1)、求该抛物线的解析式；

(2)、求该抛物线的对称轴；

(3)、点P是该抛物线对称轴上一点，且△POA是等腰三角形，求出点P的坐标．

查看试题解析