广西壮族自治区贵港市港南区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 在函数 图像上的点是( )A、 B、 C、 D、2. 若sinα= ,则锐角α=( )A、30° B、45° C、50° D、60°3. 关于x的一元二次方程有实数根,则的取值范围是( )A、 B、 C、且 D、且4. 方程x2﹣2x=0的根是( )A、x=﹣2 B、x1=0,x2=2 C、x=2 D、x1=0,x2=﹣25. 一元二次方程5x2﹣3x=x+1化为一般形式ax2+bx+c=0(a≠0)后,a,b,c的值分别是( )A、a=5,b=﹣4,c=﹣1 B、a=5,b=4,c=1 C、a=4,b=﹣5,c=1 D、a=﹣5,b=4,c=﹣16. 若a,b为方程 的两个实数根,则2 的值为( )A、-41 B、-35 C、39 D、457. 在△ABC中,已知∠A、∠B均为锐角,且有|tan2B﹣3|+(2sinA﹣ )2=0,则△ABC是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、钝角三角形8. 某校为落实“光盘行动”,对每天的剩饭菜进行称重,第一周的剩余量为20kg,第三周为9.8kg,设每周剩余量的平均减少率为x,则可列方程( )A、20(1﹣x)2=9.8 B、20(1+x)2=9.8 C、20(1﹣2x)=9.8 D、20(1+2x)=9.89. 如图,点A在反比例函数 的图象上,过点A作 轴于点B,若 的面积为3,则k的值为( )
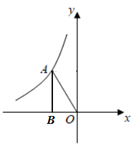 A、-6 B、6 C、-3 D、310. 如图,在 中, , ,若 的周长为 ,则 的周长是( )
A、-6 B、6 C、-3 D、310. 如图,在 中, , ,若 的周长为 ,则 的周长是( )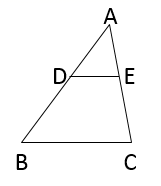 A、 B、 C、 D、11. 如图,在Rt△ABC中,∠ACB = 90°,AC = BC = 4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为( )
A、 B、 C、 D、11. 如图,在Rt△ABC中,∠ACB = 90°,AC = BC = 4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为( ) A、 B、 C、 D、12. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC.其中正确的个数是( )
A、 B、 C、 D、12. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC.其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 空气是混合物,为直观介绍空气各成分的百分比,宜选用统计图.(填“扇形”、“条形”或“折线”)14. 代数式的最小值为 .15. 如果2x=3y,那么 .16. 如图,在△ABC中,DE∥BC,且BD=2AD,若DE=2,则BC边的长为 .
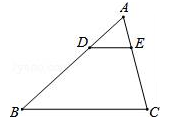 17. 如图,已知DC为∠ACB的平分线,DE∥BC.若AD=8,BD=10,BC=15,求EC的长=.
17. 如图,已知DC为∠ACB的平分线,DE∥BC.若AD=8,BD=10,BC=15,求EC的长=.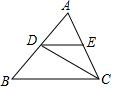 18. 图,在反比例函数y=(x>0)的图象上有点P1 , P2 , P3 , P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则阴影部分的面积S1+S2+S3+S4= .
18. 图,在反比例函数y=(x>0)的图象上有点P1 , P2 , P3 , P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则阴影部分的面积S1+S2+S3+S4= .
三、解答题
-
19.(1)、计算:()﹣1﹣2tan45°+4sin60°﹣;(2)、解方程:x2﹣2x﹣3=0.20. 已知 ,且 ,求 的值.21. 如图,在▱ABCD中,设BC边的长为x(cm),BC边上的高线AE长为y(cm),已知▱ABCD的面积等于24cm2 .
 (1)、求y关于x的函数表达式;(2)、求当3<y<6时x的取值范围.22. 如图,在 中, , , ,求 的面积.
(1)、求y关于x的函数表达式;(2)、求当3<y<6时x的取值范围.22. 如图,在 中, , , ,求 的面积. 23. 某店只销售某种进价为40元/kg的特产. 已知该店按60元/kg 出售时,平均每天可售出100kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10kg.若该店销售这种特产计划平均每天获利2240元.(1)、每千克该特产应降价多少元?(2)、为尽可能让利于顾客,则该店应按原售价的几折出售?24. 如图,在 中, 为 上一点, .
23. 某店只销售某种进价为40元/kg的特产. 已知该店按60元/kg 出售时,平均每天可售出100kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10kg.若该店销售这种特产计划平均每天获利2240元.(1)、每千克该特产应降价多少元?(2)、为尽可能让利于顾客,则该店应按原售价的几折出售?24. 如图,在 中, 为 上一点, .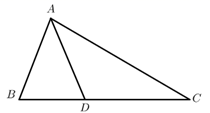 (1)、求证: .(2)、若 ,求 的长.25. 如图,一次函数 的图像与反比例函数 的图像相交于A( )、B( )两点。
(1)、求证: .(2)、若 ,求 的长.25. 如图,一次函数 的图像与反比例函数 的图像相交于A( )、B( )两点。 (1)、求反比例函数和一次函数的解析式;(2)、求直线AB与x轴的交点C的坐标及△AOB的面积;(3)、根据图像直接写出使一次函数的值大于反比例函数的值的 的取值范围26. 阅读材料:
(1)、求反比例函数和一次函数的解析式;(2)、求直线AB与x轴的交点C的坐标及△AOB的面积;(3)、根据图像直接写出使一次函数的值大于反比例函数的值的 的取值范围26. 阅读材料:对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)、已知 ,若 ,则当 时, 有最小值,最小值为;(2)、已知 ,若 ,则 取何值时, 有最小值,最小值是多少?(3)、用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?