广西壮族自治区崇左市宁明县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线y＝﹣（x+1）²﹣2的对称轴是（）

A、x＝1 B、x＝﹣1 C、x＝2 D、x＝﹣2

查看试题解析
2. 下列说法中，错误的是（）

A、等边三角形都相似 B、等腰直角三角形都相似 C、矩形都相似 D、正方形都相似

查看试题解析
3. 若二次函数y＝x²﹣2x+a有最小值为6，则a的值为（）

A、﹣6 B、6 C、﹣7 D、7

查看试题解析
4. 下列关于二次函数 $y = 2 x^{2}$ 的说法正确的是（）

A、它的图象经过点 $(- 1, - 2)$ B、它的图象的对称轴是直线 $x = 2$ C、当 $x < 0$ 时， $y$ 随 $x$ 的增大而减小 D、当 $x = 0$ 时， $y$ 有最大值为0

查看试题解析
5. 抛物线y＝x²+1经过平移得到抛物线y＝（x+1）² ，平移的方法是（）

A、向左平移1个，再向下平移1个单位 B、向右平移1个，再向下平移1个单位 C、向左平移1个，再向上平移1个单位 D、向右平移1个，再向上平移1个单位

查看试题解析
6. 在比例尺是1∶38000的黄浦江交通游览图上，某隧道长约7 cm，则它的实际长度约为（）

A、266 km B、26.6 km C、2.66 km D、0.266 km

查看试题解析
7. 下列函数中，当x＞0时，y随x的增大而减小的是（）

A、y＝ $\frac{2}{x}$ B、y＝ $\frac{x}{2}$ C、y＝3x+2 D、y＝x²﹣3

查看试题解析
8. 如图，已知一次函数y＝kx﹣3（k≠0）的图象与x轴，y轴分别交于A，B两点，与反比例函数 $y = \frac{12}{x}$ （x＞0）交于C点，且AB＝AC，则k的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、 $\frac{7}{2}$

查看试题解析
9. 反比例函数 $y = \frac{- k^{2} - 1}{x}$ 图象上有三个点（x₁ ， y₁），（x₂ ， y₂），（x₃ ， y₃），其中x₁＜0 ＜x₂ ＜x₃ ，则y₁ ，y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₃＜y₁ C、y₁＜y₃＜y₂ D、y₃＜y₂＜y₁

查看试题解析
10. 如图，点G、F分别是 $△ B C D$ 的边 $B C$ 、 $C D$ 上的点， $B D$ 的延长线与 $G F$ 的延长线相交于点A ， $D E / / B C$ 交 $G A$ 于点E ，则下列结论错误的是（）

A、 $\frac{A D}{B D} = \frac{A E}{E G}$ B、 $\frac{D E}{C G} = \frac{D F}{C F}$ C、 $\frac{A E}{A G} = \frac{D E}{B C}$ D、 $\frac{A D}{A B} = \frac{D E}{B G}$

查看试题解析
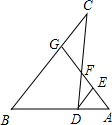11. 如图1，物理课上学习过利用小孔成像说明光的直线传播．现将图1抽象为图2，其中线段AB为蜡烛的火焰，线段A′B′为其倒立的像．如果蜡烛火焰AB的高度为2cm，倒立的像A′B′的高度为5cm，线段OA的长为4cm，那么线段OA′的长为（）

A、4cm B、5cm C、8cm D、10cm

查看试题解析
12. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，下列结论：①b＜0；②c＞0；③a+c＞﹣b；④b²﹣4ac＞0，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

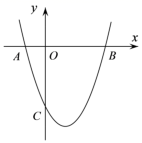
13. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，且2a+b+c＝33，则a﹣b+c＝．

查看试题解析
14. 二次函数y＝x²﹣2x+3图象与y轴的交点坐标是.

查看试题解析
15. 二次函数y＝ax²+bx+c的图象如图所示，那么abc0（填“＞”，“＝”，或“＜”）．

查看试题解析
16. 已知反比例函数 $y = \frac{k - 1}{x}$ 的图象经过点 $(2 ， - 4)$ ，则 $k$ 的值为．

查看试题解析
17. 下列函数：①y＝3x²；②y＝-3（x+3）²；③y＝-3x²-1；④y＝-2x²+5；⑤y＝-（x-1）² ，其中函数图象形状、开口方向相同的是.

查看试题解析
18. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么AP的长度为cm．

查看试题解析

三、解答题

19. 已知a、b、c为△ABC的三边长，且 $a + b + c = 48$ ， $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，求△ABC三边的长．

查看试题解析
20. 已知抛物线y=﹣x²﹣3x+t经过A（0，3）．

(1)、求抛物线的解析式；

(2)、设点P（m，n）在该抛物线上，求m+n的最大值．

查看试题解析
21. 如图，反比例函数y₁＝ $\frac{k}{x}$ 的图象与一次函数y₂＝ $\frac{1}{4}$ x的图象交于点A，B，点B的横坐标实数4，点P（1，m）在反比例函数y₁＝ $\frac{k}{x}$ 的图象上．

(1)、求反比例函数的表达式；

(2)、观察图象回答：当x为何范围时，y₁＞y₂ ．

查看试题解析
22. 如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．

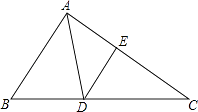(1)、求证：△DCE∽△BCA；

(2)、若AB=3，AC=4．求DE的长．

查看试题解析
23. 已知二次函数y =x² + 4x + 3．

(1)、将二次函数的表达式化为y = a （x-h）²+ k 的形式；

(2)、在平面直角坐标系xOy中，用描点法画出这个二次函数的图象；
x
…
…
y
…
…

(3)、观察图象，直接写出当 $- 3 \leq x \leq 0$ 时 $y$ 的取值范围；

(4)、根据（2）中的图象，写出一条该二次函数的性质．

查看试题解析
24. 为满足市场需求，某超市在八月十五“中秋节”来临前夕，购进一种品牌的月饼，每盒进价40元，根据以往的销售经验发现：当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

(1)、写出每天的销售量 $y ($ 盒 $)$ 与每盒月饼上涨 $x ($ 元 $)$ 之间的函数关系式．

(2)、当每盒售价定为多少元时，当天的销售利润 $W ($ 元 $)$ 最大？最大利润是多少？

(3)、为稳定物价，有关管理部门限定，这种月饼每盒的利润不得高于进价的 $30 %$ ，那么超市每天获得最大利润是多少？

查看试题解析
25. 如图，矩形ABCD中，已知AB＝6．BC＝8，点E是射线BC上的一个动点，连接AE并延长，交射线DC于点F．将△ABE沿直线AE翻折，点B的对应点为点B′．

(1)、如图1，若点E为线段BC的中点，延长AB′交CD于点M，求证：AM＝FM；

(2)、如图2，若点B′恰好落在对角线AC上，求 $\frac{B E}{C E}$ 的值．

查看试题解析
26. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于两点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ．

(1)、求 $b$ ， $c$ 的值．

(2)、观察函数的图象，直接写出当 $x$ 取何值时， $y > 0$ ．

(3)、设抛物线交 $y$ 轴于点 $C$ ，在该抛物线的对称轴上是否存在点 $Q$ ，使得 $△ Q A C$ 的周长最小？若存在，求出 $Q$ 点的坐标；若不存在，请说明理由．

查看试题解析

x	…						…
y	…						…