广西壮族自治区北海市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{4}$ 的结果是（）

A、±2 B、2 C、 $\pm \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
2. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\frac{1}{\sqrt{2}}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{5}$

查看试题解析
3. 如图，将□ABCD的一边BC延长至点E ，若∠A＝110°，则∠1等于（）

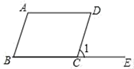A、110° B、35° C、70° D、55°

查看试题解析
4. 下列各组数中，不是勾股数的是（）

A、3，4，5 B、30，40，50 C、7，14，15 D、5，12，13

查看试题解析
5. 一次函数y＝﹣2x+b的图象经过点A（2，y₁），B（﹣1，y₂），则y₁与y₂的大小关系正确的是（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、无法确定

查看试题解析
6. 11名同学参加数学竞赛初赛，他们的等分互不相同，按从高分录到低分的原则，取前6名同学参加复赛，现在小明同学已经知道自己的分数，如果他想知道自己能否进入复赛，那么还需知道所有参赛学生成绩的（　　）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 如图，某游客为爬上3千米的山顶看日出，先用1小时爬了2千米，休息0.5小时后，再用1小时爬上山顶，游客爬山所用时间t（小时）与山高h（千米）间的函数关系用图象表示是（）

A、 B、B C、 D、

查看试题解析
8. 如图，点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点．则下列说法：
①若AC＝BD，则四边形EFGH为矩形；

②若AC⊥BD，则四边形EFGH为菱形；

③若四边形EFGH是平行四边形，则AC与BD互相平分；

④若四边形EFGH是正方形，则AC与BD互相垂直且相等．

其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 若实数x，y满足y＝ $\sqrt{2 x - 1} + \sqrt{2 - 4 x}$ ﹣2020，则4x﹣y的值为（　　）

A、2021 B、2022 C、2023 D、2024

查看试题解析
10.
直线y＝ $\frac{2}{3}$ x＋4与x轴、y轴分别交于点A和点B ，点C ， D分别为线段AB ， OB的中点，点P为OA上一动点，PC＋PD值最小时点P的坐标为（）.

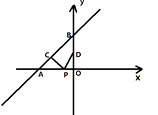A、(－3，0) B、(－6，0) C、(－ $\frac{5}{2}$ ，0) D、(－ $\frac{3}{2}$ ，0)

查看试题解析
11. 如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB＝2，BC＝1，则顶点C到坐标原点O的最大距离为（）

A、1+ $\sqrt{2}$ B、1+ $\sqrt{3}$ C、3 D、 $\sqrt{5}$

查看试题解析

二、填空题

12. 若 $\sqrt{a - 5}$ +（b+2）²＝0，则a+b＝.

查看试题解析
13. 已知菱形的边长为4，一个内角为60°，则菱形较短的对角线长为．

查看试题解析
14. 已知一组数据3，a，4，6，7，它们的平均数是5，则这组数据的方差是．

查看试题解析
15. 如图，函数 $y = k x$ 与 $y = - \frac{3}{2} x + b$ 的图象交于点 $M (- 2 ， 1)$ ，那么不等式 $k x > - \frac{3}{2} x + b$ 的解集是．

查看试题解析
16. 如图，四边形ABCD是正方形，点G是边BC上一点，DE⊥AG于点E，BF∥DE，且交AG于点F．已知DE＝10，BF＝6，则EF的长度为．

查看试题解析
17. 一次函数y＝﹣mx+n的图象经过二、三、四象限，则化简 $\sqrt{(m - n)^{2}} + \sqrt{n^{2}}$ 所得的结果是．

查看试题解析
18. 如图，▱ABCD的对角线AC与BD相交于点O，AE⊥BC，垂足为E，AB＝2，BD＝4 $\sqrt{2}$ ， AC＝4，则AE的长为．

查看试题解析
19. 在平面直角坐标系中有两点 $A (- 1 ， 2)$ ， $B (2 ， 3)$ ，如果函数 $y = k x - 1$ 的图象与线段 $A B$ 的延长线相交（交点不包括点B），则实数k的取值范围是.

查看试题解析

三、解答题

20. 计算： $(\sqrt{2} + 1) (\sqrt{2} - 1) - (\frac{\sqrt{2}}{2})^{0} - | 1 - \sqrt{2} | + \frac{\sqrt{3} + \sqrt{6}}{\sqrt{3}}$

查看试题解析
21. 如图，在ΔABC中，CD⊥AB于点D，AC=20，BC=15，DB=9，

(1)、求DC的长；

(2)、求证：ΔABC是直角三角形.

查看试题解析
22. 如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OA，OC的中点，连接BE，DE，BF，DF．

(1)、求证：四边形BEDF是平行四边形；

(2)、若AC＝2BD，请判断四边形BEDF的形状，并说明理由．

查看试题解析
23. 2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛．经过初赛、复赛，选出了两个代表队参加市内7月份的决赛．两个队各选出的5名选手的复赛成绩如图所示。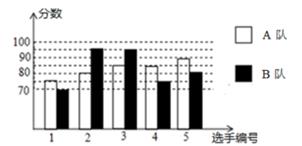

(1)、根据图示补全下表；

平均数(分)

中位数(分)

众数(分)

A队

83

85

B队

95

(2)、结合两队成绩的平均数和中位数，分析哪个队的复赛成绩较好；

(3)、计算两队成绩的方差，并判断哪一个代表队选手成绩较为稳定。

查看试题解析
24. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象与y轴交于点 $A$ （0，4），与直线 $y = - \frac{1}{3} x - 1$ 在第四象限相交于点B，连接OB， $△ A O B$ 的面积为6．

(1)、求点B的坐标及直线AB的解析式；

(2)、已知点M在直线AB右侧，且△MAB是以AB为直角边的等腰直角三角形．请求出符合条件的点M的坐标．

查看试题解析
25. 如图1，在▱ABCD中，AB＝14，AD＝8，∠DAB＝60°，对角线AC，BD交于点O．一动点P在边AB上由A向B运动（不与A，B重合），连接PO并延长，交CD于点Q．

(1)、求证：OP＝OQ；

(2)、过点D作DE⊥AB于点E，画出图形并求出线段DE的长度；

(3)、当AP＝9时，求线段OP的长度；

(4)、连接AQ，PC，如图2，随着点P的运动，四边形APCQ可能是菱形吗？如果可能，请求出此时线段AP的长度；如果不可能，请说明理由．

查看试题解析

	平均数(分)	中位数(分)	众数(分)
A队	83	85
B队			95