安徽省蚌埠市淮上区2022年小升初数学试卷
试卷更新日期：2022-10-12 类型：小升初真题
一、选择（每题2分，共10分）
-
1. 任意两个奇数相乘，积一定是（ ）。A、合数 B、质数 C、奇数2. 王老师统计了六（1）班五次测试每次优秀人数占全班总人数的百分比，分别是37.5%、50%、52.5%、55%、62.5%。用什么统计图表示比较合适？（ ）A、扇形统计图 B、折线统计图 C、条形统计图3. 下列选项中，能用“2a+6”表示的是（ ）。A、
整条线段的长度
B、
这个长方形的周长
C、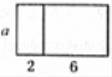
这个图形的面积
4. 一辆行驶中的小汽车前轮压碎了一个苹果，在路上留下了几个印记（如图）。苹果与第一个印记之间的距离大约是2米。这个“2米”表示（ ）。
A、车轮的周长 B、小汽车的车长 C、前后车轮之间的距离5. 如图，A、B、C三个小岛的位置正好构成了一个直角三角形。那么A岛在B岛的（ ）。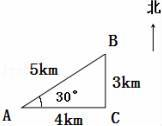
A、南偏西30°方向5千米处 B、北偏东60°方向5千米处 C、南偏西60°方向5千米处二、填空（6-14题每空1分，15题3分，共25分）
-
6. 8个千万、6个千和4个千分之一组成的数是 ， 改写成用“亿”作单位，并保留两位小数是 亿。7. 20÷＝＝0.8＝：20＝%。8. 20秒＝分 5.34千克＝克
64000平方米＝公顷 4.2升＝毫升
9. 把a米长的钢筋锯成同样长的4段，每段长是全长的 ， 每段长米。10. 用边长1分米的小正方体搭成一个模型，从正面看是
， 从上面看是
， 从侧面看是 ， 这个模型的体积是立方分米。 11. a的等于b的 ， 求a与b的最简比。在写出等式a×＝b×后，小华和小明使用了两种不同的方法。(1)、小华假设了一个具体的数值。例如，假设等号两边的积都等于1，那么，a＝ ， b＝ ， a与b的最简比是 。(2)、小明运用比例的基本性质，根据上面的等式直接写出比例a：b＝ ， 再化简成最简比就可以。12. 如图：如果点X的位置表示为（2，3），则点Y的位置可以表示为。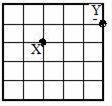
13. 如图像表示一个水龙头打开后出水量与时间的关系。
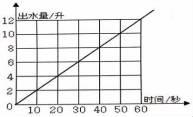(1)、这个水龙头打开后的出水量和时间成 比例。(2)、出水8升要用 秒，35秒能出水 升。14. 笼子里有若干只鸡和兔。从上面数，有35个头，从下面数，有94只脚。下面说法正确的有 。（填序号）①鸡兔一共有35只。
②假如全是鸡，就会少24只脚。
③假如全是兔，就会多24只脚。
④如果它们都抬起2只脚，剩下站在地上的24只脚就都是兔子的。
15. 小猫每天大约睡12个小时，它的一生大概有50%的时间在睡觉。考拉每天大约睡18个小时，比小猫的睡眠时间大约长 %，它的一生大概有 %的时间在睡觉。三、计算（26分）
-
16. 直接写出得数。
1÷＝ ＝ 1.1+0.11＝ 2.4×50%＝ 0.24÷0.8＝
＝ 8×＝ 10﹣0.99＝ 0.22＝ 4×25%÷4×25%＝
17. 计算下面各题（能简算的要简算）。①210÷35+12×109
②2.5×1.25×16
③（）×12
④ [（）]
18. 求未知数。(1)、 ＝(2)、 ：＝：x(3)、 x﹣x＝四、操作（9分）
-
19. 操作
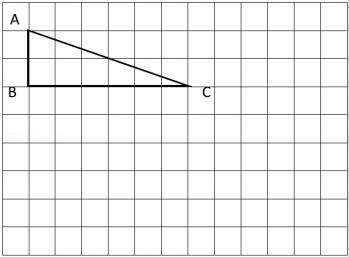(1)、把三角形绕点B顺时针旋转90°，画出旋转后的图形。(2)、画一个与三角形ABC面积相等的平行四边形。(3)、按1：2的比画出三角形ABC缩小后的图形。缩小后的图形与原图周长的比是 ， 面积的比是 。20. 甲、乙、丙、丁四个好朋友在一起讨论体重问题。甲的体重是52千克，如果以四人的平均体重为标准，则甲的体重记为“+6”千克，可用如图中的直条表示。
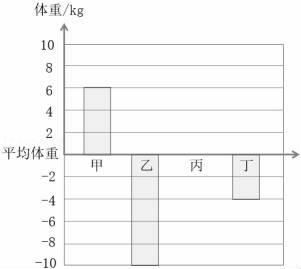(1)、这四人的平均体重是 千克。(2)、从图中可知，乙的体重记为 千克，乙与丁相比，瘦一些。(3)、在图中画出表示丙体重的直条。五、解决实际问题（每题5分，共30分）
-
21. 龟兔赛跑，全程2000米。乌龟每分钟爬行25米，兔子每分钟跑500米。兔子见乌龟慢吞吞的，心生傲慢，便在途中睡了一觉，醒来发现乌龟已遥遥领先，慌忙起身，奋起直追，最终与乌龟同时到达终点。兔子在途中睡了多长时间？22. 在同一幅地图上，量得甲、乙两地的直线距离是20厘米，甲、丙两地的直线距离是12厘米。如果甲、乙两地的实际距离是1600千米，那么甲丙两地的实际距离是多少？23. 书店的图书凭优惠卡可打八折，小明用优惠卡买了一套书、省了9.6元。这套书原价多少钱？24. 食堂运来495千克煤，已经用了三天，剩下的比已经用去的多45千克。这个食堂平均每天用煤多少千克？25. 天气炎热，兰兰从冰箱里拿出一瓶雪碧招待来家做客的东东和亮亮．这瓶雪碧能倒满2个这样的水杯吗？（直径和高均为水杯里面测得的数据）
26. 我国一些地标性建筑的外形很有特色。例如，广州塔因其身姿婀娜被称为“小蛮腰”；北京的“中国尊”，其外形是依照我国古代盛酒的器具“尊”设计的。中国尊的高度为528米，比广州塔矮 ， 广州塔的高度是多少米？
六、附加题（每题5分，共10分）
-
27. 一个平面图形经过平移或旋转可以形成立体图形。例如，分别将长方形、圆作为底面，向上平移可以得到长方体、圆柱（如图1），它们的体积均可以用“底面积×高”进行计算；将一个长4厘米，宽3厘米的长方形，绕着长旋转一周，可以得到一个圆柱（如图2）。
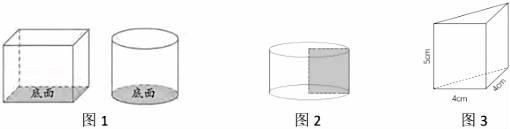(1)、将一个底面直径 厘米的圆作为底面，向上平移 厘米，也可以形成图2中的圆柱。(2)、将一个两条直角边均为4厘米的直角三角作为底面，向上平移5厘米，形成一个立体图形（如图3），它体积是多少立方厘米？28. 甲、乙两仓库存放大米质量的比是3：7，甲仓库运进6吨，乙仓库运出4吨后，甲、乙两仓库大米质量比变为3：5。两个仓库原来各有大米多少吨？