广西河池市环江县2021-2022学年九年级上学期期中测试数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 下列平面图形中是中心对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 方程的解是( )A、 B、 C、 , D、 ,3. 将方程时,化方程为一般式,各项系数、、依次是( )A、3, , 1 B、3, , C、3,3, D、3,3,14. 方程配方后所得的方程是( )A、 B、 C、 D、5. 下面的函数是二次函数的是( )A、 B、 C、 D、6. 函数的图象与轴的交点坐标为( ).A、 B、 C、 D、7. 函数y=x2+2x﹣4的顶点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列关于二次函数 ,下列说法正确的是( ).A、它的开口方向向下 B、它的顶点坐标是 C、当 时, 随 的增大而增大 D、当 时, 有最小值是39. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小10. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>111. 函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的( )A、
2. 方程的解是( )A、 B、 C、 , D、 ,3. 将方程时,化方程为一般式,各项系数、、依次是( )A、3, , 1 B、3, , C、3,3, D、3,3,14. 方程配方后所得的方程是( )A、 B、 C、 D、5. 下面的函数是二次函数的是( )A、 B、 C、 D、6. 函数的图象与轴的交点坐标为( ).A、 B、 C、 D、7. 函数y=x2+2x﹣4的顶点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列关于二次函数 ,下列说法正确的是( ).A、它的开口方向向下 B、它的顶点坐标是 C、当 时, 随 的增大而增大 D、当 时, 有最小值是39. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小10. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>111. 函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的( )A、 B、
B、 C、
C、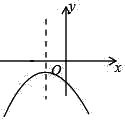 D、
D、 12. 某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
12. 某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( ) A、180(1﹣x)2=461 B、180(1+x)2=461 C、368(1﹣x)2=442 D、368(1+x)2=442
A、180(1﹣x)2=461 B、180(1+x)2=461 C、368(1﹣x)2=442 D、368(1+x)2=442二、填空题
-
13. 方程x2=2的解是 .
14. 点A(﹣2,3)关于原点对称的点的坐标是 .15. 某人感染了某种病毒,经过两轮传染共感染了121人.设该病毒一人平均每轮传染x人,则关于x的方程为 .16. 将抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是 .17. 抛物线与x轴的公共点是 , 则这条抛物线的对称轴是直线= .18. 如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 .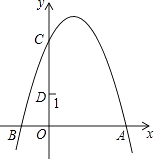
三、解答题
-
19. 解方程: .20. 解方程:x2+2x﹣3=0.21. 用配方法解方程: .22. 如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A'B'C′,
 (1)、画出△A'B'C'.(2)、写出下列各点的坐标A' ▲ , B′ ▲ , C′ ▲ .23. 已知二次函数 .
(1)、画出△A'B'C'.(2)、写出下列各点的坐标A' ▲ , B′ ▲ , C′ ▲ .23. 已知二次函数 . (1)、求这个二次函数图象与轴的交点坐标、与轴的交点坐标.(2)、画出这个二次函数图象.24. 一名男生推铅球,铅球的行进高度 (单位: )与水平距离 (单位: )之间的关系为 ,铅球行进路线如图.
(1)、求这个二次函数图象与轴的交点坐标、与轴的交点坐标.(2)、画出这个二次函数图象.24. 一名男生推铅球,铅球的行进高度 (单位: )与水平距离 (单位: )之间的关系为 ,铅球行进路线如图.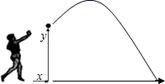 (1)、求出手点离地面的高度.(2)、求铅球推出的水平距离.(3)、通过计算说明铅球的行进高度能否达到4 .
(1)、求出手点离地面的高度.(2)、求铅球推出的水平距离.(3)、通过计算说明铅球的行进高度能否达到4 .

