广西百色市靖西市2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 二次函数 的图象是( )A、线段 B、直线 C、抛物线 D、双曲线2. 已知2x=3y , 则下列比例式成立的是( )A、 B、 C、 D、3. 若y=(a﹣2)x2﹣3x+2是二次函数,则a的取值范围是( )A、a≠2 B、a>0 C、a>2 D、a≠04. 已知线段a,b,c,d是比例线段,其中 , , , 则d等于( )A、 B、 C、 D、5. 已知反比例函数 的图象过点 则该反比例函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限6. 已知△ABC∽△A′B′C′,AD和A′D′是对应高,且AD:A′D′=2,则它们的周长比是( )A、1:2 B、2:1 C、1:4 D、4:17. 如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是( )A、
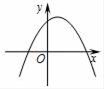 B、
B、 C、
C、 D、
D、 8. 如图,已知AB∥CD∥EF,AC=6,CE=2,BD=4,则DF的值为( )
8. 如图,已知AB∥CD∥EF,AC=6,CE=2,BD=4,则DF的值为( )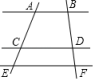 A、 B、 C、 D、19. 二次函数y=(x+4)2+5的图象的开口方向、对称轴、顶点坐标分别是( )A、向上,直线x=4,(4,5) B、向下,直线x=﹣4,(﹣4,5) C、向上,直线x=4,(4,﹣5) D、向上,直线x=﹣4,(﹣4,5)10. 已知线段 , 点P是线段的黄金分割点(),则线段的长为( )A、 B、 C、 D、11. 已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )A、k>﹣1 B、k>﹣1且k≠0 C、k≥﹣1 D、k≥﹣1且k≠012. 如图,在中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断∽的是( ).
A、 B、 C、 D、19. 二次函数y=(x+4)2+5的图象的开口方向、对称轴、顶点坐标分别是( )A、向上,直线x=4,(4,5) B、向下,直线x=﹣4,(﹣4,5) C、向上,直线x=4,(4,﹣5) D、向上,直线x=﹣4,(﹣4,5)10. 已知线段 , 点P是线段的黄金分割点(),则线段的长为( )A、 B、 C、 D、11. 已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )A、k>﹣1 B、k>﹣1且k≠0 C、k≥﹣1 D、k≥﹣1且k≠012. 如图,在中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断∽的是( ).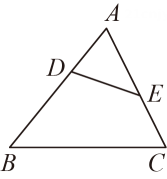 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
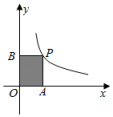
13. 已知a=3,b=27,则a,b的比例中项为14. 如图,P是反比例函数图象上一点,矩形OAPB的面积是7,则k= .
 15. 如图是一个边长为1的正方形组成的网格,与都是格点三角形(顶点在网格交点处),并且 , 则与的面积比是 .
15. 如图是一个边长为1的正方形组成的网格,与都是格点三角形(顶点在网格交点处),并且 , 则与的面积比是 .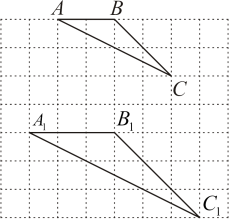 16. 假设飞机着陆后滑行的距离y(单位:米)关于滑行时间t(单位:秒)满足函数关系式y=60t﹣t2 , 则经过 秒后,飞机停止滑行.17. 已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=1,则不等式ax2+bx+c>0的解集是 .
16. 假设飞机着陆后滑行的距离y(单位:米)关于滑行时间t(单位:秒)满足函数关系式y=60t﹣t2 , 则经过 秒后,飞机停止滑行.17. 已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=1,则不等式ax2+bx+c>0的解集是 .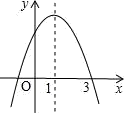 18. 已知y=x2+2kx+k﹣1,当﹣1<x<2时,有最小值﹣1,则k的值为 .
18. 已知y=x2+2kx+k﹣1,当﹣1<x<2时,有最小值﹣1,则k的值为 .三、解答题
-
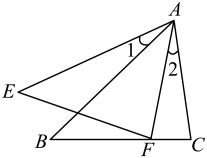
19. 如果(b+d+f≠0),且a+c+e=5(b+d+f).求k的值.20. 画函数y=(x﹣2)2﹣1的图象,并根据图象回答:(1)、当x为何值时,y随x的增大而减小.(2)、当x为何值时,y>0.21. 如图,AB•AF=AE•AC,且∠1=∠2,求证:△ABC∽△AEF.
 22. 某气球内充满了一定量的气体,当温度不变时,气球内气体的压强p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
22. 某气球内充满了一定量的气体,当温度不变时,气球内气体的压强p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.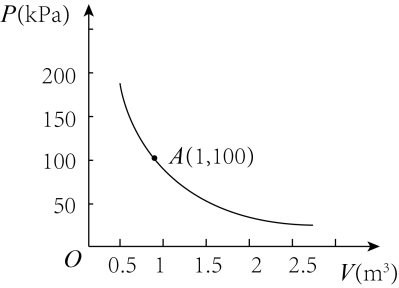 (1)、求这一函数的表达式;(2)、当气体压强为50kPa时,求V的值;(3)、当气球内的体积小于0.5m3时,气球爆炸,为了安全起见,气体的压强不大于多少?23. 如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥的跨度为12m,桥洞与水面的最大距离是6m,桥洞两侧壁上各有一盏距离水面4m的景观灯,求两盏景观灯之间的水平距离(提示:请建立平面直角坐标系后,再作答).
(1)、求这一函数的表达式;(2)、当气体压强为50kPa时,求V的值;(3)、当气球内的体积小于0.5m3时,气球爆炸,为了安全起见,气体的压强不大于多少?23. 如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥的跨度为12m,桥洞与水面的最大距离是6m,桥洞两侧壁上各有一盏距离水面4m的景观灯,求两盏景观灯之间的水平距离(提示:请建立平面直角坐标系后,再作答).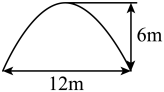 24. 在比例尺是1:3000000的地图上,量得两地之间的距离是10厘米,甲、乙两车同时从两地相向而行,2小时后,两车相遇,已知甲、乙两车的速度比是3:2,甲、乙两车的速度各是多少?25. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上、已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
24. 在比例尺是1:3000000的地图上,量得两地之间的距离是10厘米,甲、乙两车同时从两地相向而行,2小时后,两车相遇,已知甲、乙两车的速度比是3:2,甲、乙两车的速度各是多少?25. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上、已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.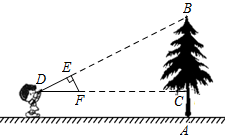 26. 如图,直线y=x+2与抛物线y=ax2-8x+6(≠0)相交于A(4,6)和B( , ),点P是线段AB上异于A、B的动点,过点P作PD⊥x轴于点E,交抛物线于点D.
26. 如图,直线y=x+2与抛物线y=ax2-8x+6(≠0)相交于A(4,6)和B( , ),点P是线段AB上异于A、B的动点,过点P作PD⊥x轴于点E,交抛物线于点D.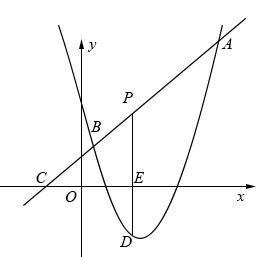 (1)、求抛物线的解析式;(2)、当D为抛物线顶点的时候,求△ADC的面积;(3)、是否存在这样的点P,使△ADC的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当D为抛物线顶点的时候,求△ADC的面积;(3)、是否存在这样的点P,使△ADC的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.