广西百色市德保县2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 若关于x的函数y=(2﹣a)x2﹣x是二次函数,则a的取值范围是( )A、a≠0 B、a≠2 C、a<2 D、a>22. 下列函数中,表示y是x的反比例函数的是( )A、 B、 C、 D、3. 把二次函数化成的形式,正确的是( )A、 B、 C、 D、4. 函数与的图象的不同之处是( )A、顶点 B、对称轴 C、开口方向 D、形状5. 如果线段a=2cm,b=18cm,那么a和b的比例中项是( )A、3cm B、4cm C、±6cm D、6cm6. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、7. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
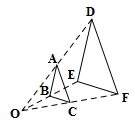 A、1∶2 B、1∶3 C、1∶4 D、1∶58. 若双曲线的图象经过第二、四象限,则k的取值范围是( )A、 B、 C、 D、9. 如图,在 中, , , , ,则 的长为( )
A、1∶2 B、1∶3 C、1∶4 D、1∶58. 若双曲线的图象经过第二、四象限,则k的取值范围是( )A、 B、 C、 D、9. 如图,在 中, , , , ,则 的长为( )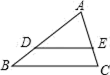 A、6 B、7 C、8 D、910. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )
A、6 B、7 C、8 D、910. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )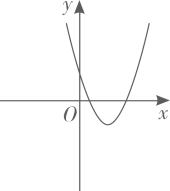 A、
A、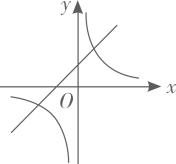 B、
B、 C、
C、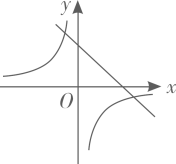 D、
D、 11. 如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( )
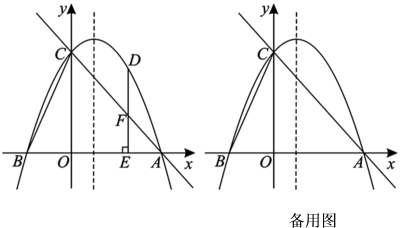
11. 如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( ) A、AB∥CD B、 C、 D、12. 如图,抛物线与轴交于点和 , 与轴交于点 . 下列结论:①;②;③;④ , 其中正确的结论个数为( )
A、AB∥CD B、 C、 D、12. 如图,抛物线与轴交于点和 , 与轴交于点 . 下列结论:①;②;③;④ , 其中正确的结论个数为( )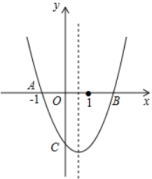 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
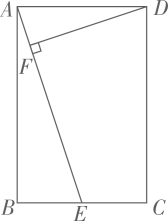
13. 已知4a=3b,则 = .14. 二次函数的顶点坐标是 .15. 若抛物线和x轴有交点,则k的取值范围是 .16. 烟花厂某种礼炮的升空高度与飞行时间的关系式是 , 若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为s.17. 如图,在Rt△ABC中,∠C=90°,点D是AC边上的一点,DE垂直平分AB,垂足为点E.若AC=8,BC=6,则线段DE的长度为.
 18. 如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数 的图象恰好经过点C,则k的值为.
18. 如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数 的图象恰好经过点C,则k的值为.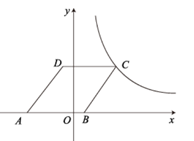
三、解答题
-
19. 已知与x成反比例,当时, , 求y与x的函数表达式.20. 已知二次函数 的图象过点 .(1)、求这个二次函数的解析式;(2)、判断点 是否在抛物线上;21. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
 (1)、以点B为位似中心,在网格内画出△A1B1C1 , 使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是 ▲ ;(2)、△A1B1C1的面积是平方单位.22. 已知 ,且x+y+z=68.求x,y,z的值.23. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .
(1)、以点B为位似中心,在网格内画出△A1B1C1 , 使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是 ▲ ;(2)、△A1B1C1的面积是平方单位.22. 已知 ,且x+y+z=68.求x,y,z的值.23. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .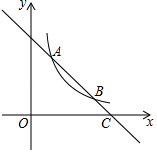 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.24. 某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.(1)、求S与x之间的函数关系式,并写出自变量x的取值范围;(2)、设计费能达到24000元吗?为什么?(3)、当x是多少米时,设计费最多?最多是多少元?
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.24. 某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.(1)、求S与x之间的函数关系式,并写出自变量x的取值范围;(2)、设计费能达到24000元吗?为什么?(3)、当x是多少米时,设计费最多?最多是多少元?