广西壮族自治区崇左市宁明县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-10-12 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中： $\frac{1}{2}$ ，﹣2² ， ﹣2.1，﹣ $\frac{1}{3}$ ，﹣π，﹣2.010010001，﹣（﹣8），0，﹣|﹣3|，负有理数的个数是（）

A、4个 B、5个 C、3个 D、2个

查看试题解析
2. 如图，检测排球，其中质量超过标准的克数记为正数，不足的克数记为负数，下面检测过的四个排球，在其上方标注了检测结果，其中质量最接近标准的一个是（）

A、 B、 C、 D、

查看试题解析
3. “比a的2倍小1的数”用代数式表示是（）

A、2（a+1） B、2（a﹣1） C、2a+1 D、2a﹣1

查看试题解析
4. 下列运算正确的是（）

A、a³+a³＝2a³ B、a³﹣a³＝a C、a³+a³＝a⁵ D、a³﹣a²＝a

查看试题解析
5. 截至2020年10月7日，全球累计新冠确诊病例约为35300000例，这个数用科学记数法表示为（）

A、 $353 \times 10^{5}$ B、 $35.3 \times 10^{6}$ C、 $3.53 \times 10^{7}$ D、 $0.353 \times 10^{8}$

查看试题解析
6. 下列运算正确的是（）

A、（﹣1）²⁰¹⁸=﹣1 B、3²=3×2=6 C、（﹣1）×（﹣3）=3 D、﹣3﹣2=﹣1

查看试题解析
7. 下列各式中，与 $x^{2} y$ 是同类项的是（）

A、 $x y^{2}$ B、 $2 x y$ C、 $- x^{2} y$ D、 $3 x^{2} y^{2}$

查看试题解析
8. 若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则7×6！的值为（）

A、42！ B、7！ C、6！ D、6×7！

查看试题解析
9. 下列去括号的结果中，正确的是（）

A、﹣3（x﹣1）＝﹣3x﹣1 B、﹣3（x﹣1）＝﹣3x+1 C、﹣3（x﹣1）＝﹣3x﹣3 D、﹣3（x﹣1）＝﹣3x+3

查看试题解析
10. 一个矩形的长是acm，周长是40cm，那么这个矩形的面积是（）

A、a（40﹣a）cm² B、a（40﹣2a）cm ² C、a（20﹣a）cm ² D、a（20+a）cm²

查看试题解析
11. 若（m﹣2）²+|n+3|＝0，则（m+n）²⁰²¹的值是（）

A、﹣1 B、1 C、2021 D、﹣2021

查看试题解析
12. 正方形ABCD在数轴上的位置如图所示，点D，A对应的数分别为0和1，若正方形ABCD绕顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为2；按此规律继续翻转下去，则数轴上数2020所对应的点是（）

A、点A B、点B C、点C D、点D

查看试题解析

二、填空题

13. ﹣2的相反数是

查看试题解析
14. 用四舍五入法把0.0158取近似数（精确到0.001）为

查看试题解析
15. 若多项式 $2 x^{3} - 8 x^{2} + x - 1$ 与多项式 $3 x^{3} + 2 m x^{2} - 5 x + 3$ 相加后不含二次项，则m的值为．

查看试题解析
16.
如图，数轴上的点P表示的数是-1，将点P向右移动3个单位长度得到点P′，则点P′ 表示的数是．

查看试题解析
17. 如图是一个计算程序，若输入a的值为-1，则输出的结果应为．

查看试题解析
18. 如图，已知直角三角形的两条直角边分别为a、b，以a为直径画一个半圆．若甲、乙两阴影部分的面积相等，则用a的代数式表示b＝

查看试题解析

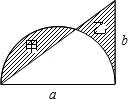
三、解答题

19. 有理数a、b、c在数轴上的位置如图所示：

(1)、判断正负，用“＞”或“＜”填空：b﹣1；a1；cb．

(2)、化简：|b+1|+|a﹣1|﹣|c﹣b|．

查看试题解析
20. 先化简，再求值：﹣2x+xy﹣[﹣2（4xy+x）+xy]，其中x＝﹣ $\frac{1}{2}$ ， y＝﹣1．

查看试题解析
21. 计算：

(1)、 ${(- 3)}^{3} \div 2 \frac{1}{4} \times {(- \frac{2}{3})}^{2}$ ；

(2)、8﹣2³÷（﹣4）×|2﹣（﹣3）²|．

查看试题解析
22. 化简：

(1)、x²y﹣3xy²+2yx²﹣y²x；

(2)、3（m﹣3n）+2（2m﹣2n）．

查看试题解析
23. 如图，某文化休闲广场的四角都设计一块半径相同的四分之一圆的花坛，若圆形的半径为 $r$ 米，广场长为 $a$ 米，宽为 $b$ 米．

(1)、请列式表示广场空地的面积：平方米；

(2)、若休闲广场的长为150米，宽为100米，圆形花坛的半径为20米，求广场空地的面积（ $π$ 取3.14）．

查看试题解析
24. 阅读计算过程：
$3 \frac{1}{3} - 2^{2} \div [{(\frac{1}{2})}^{2} - (- 3 + 0.75)] \times 5$
解：原式＝ $3 \frac{1}{3} - 2^{2} \div [\frac{1}{4} - 3 + \frac{3}{4}] \times 5$ ①
＝ $3 \frac{1}{3} + 4 \div (- 2) \times 5$ ②
＝ $3 \frac{1}{3} + \frac{2}{5}$ ③
＝ $3 \frac{11}{15}$
回答下列问题：

(1)、步骤①错在；

(2)、步骤①到步骤②错在；

(3)、步骤②到步骤③错在；

(4)、此题的正确结果是．

查看试题解析

25. 从2开始，连续的偶数相加，它们和的情况如下表：

加数的个数n	S
1	2=1×2
2	2＋4=6=2×3
3	2＋4＋6=12=3×4
4	2＋4＋6＋8=20=4×5
5	2＋4＋6＋8＋10=30=5×6

(1)、若n=8时，则S的值为．

(2)、根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n= ．

(3)、根据上题的规律计算2+4+6+8+10+…+98+100

的值．

查看试题解析

26. 某商场计划投入一笔资金采购一批商品，经过市场调查发现，有两种销售方式：
方式一：如果月末出售，可获利30%，但要付出仓储费用500元；

方式二：如果月初出售，可获利20%，并可用本金和利润再投资其他商品，到月末又可获利5%．

若商场投资本金x元，回答下列问题：

(1)、月末出售所获得的利润为元（用含 $x$ 的最简代数式表示），月初出售所获得的利润为元（用含 $x$ 的最简代数式表示）；

(2)、若商场投资本金20000元，请问选择哪种销售方式获利数多？此时获利多少元？

查看试题解析