广西壮族自治区玉林市福绵区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,为估计池塘岸边A、B的距离,小欣在池塘的一侧选取点O,测得米,米,则点A、B间的距离不可能是( )
2. 如图,为估计池塘岸边A、B的距离,小欣在池塘的一侧选取点O,测得米,米,则点A、B间的距离不可能是( ) A、22米 B、18米 C、16米 D、12米3. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、22米 B、18米 C、16米 D、12米3. 下列四个图形中,线段BE是△ABC的高的是( )A、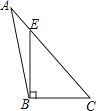 B、
B、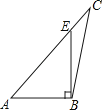 C、
C、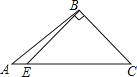 D、
D、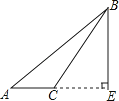 4. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=8cm,点D到AB的距离为3cm,则DB的值是( )
4. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=8cm,点D到AB的距离为3cm,则DB的值是( ) A、3cm B、8cm C、6cm D、5cm5. 下列多边形中,不能够单独铺满地面的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形6. 如图,在 中,D为 边上一点, , ,∠BAC=108°,则 的度数为( )
A、3cm B、8cm C、6cm D、5cm5. 下列多边形中,不能够单独铺满地面的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形6. 如图,在 中,D为 边上一点, , ,∠BAC=108°,则 的度数为( ) A、75° B、80° C、84° D、86°7. 已知图中的两个三角形全等,则∠1等于( )
A、75° B、80° C、84° D、86°7. 已知图中的两个三角形全等,则∠1等于( )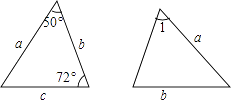 A、50° B、58° C、60° D、72°8. 已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )A、2 B、3 C、2或3 D、不能确定9. 如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB、BC于点D、E,若∠CAE=∠B+15°,则∠B的度数为( )
A、50° B、58° C、60° D、72°8. 已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )A、2 B、3 C、2或3 D、不能确定9. 如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB、BC于点D、E,若∠CAE=∠B+15°,则∠B的度数为( ) A、15° B、35° C、25° D、20°10. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A、15° B、35° C、25° D、20°10. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )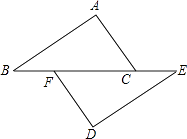 A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC11. 已知∠AOB=30°,点P在∠AOB内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2的形状一定是( )A、直角三角形 B、等边三角形 C、底边和腰不相等的等腰三角形 D、钝角三角形12. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边 DCE,AD与BE交于点O,AD与BC交于点 ,BE与CD交于点Q,连接PQ,以下五个结论:① ACD≌ BCE;②CP=CQ;③PQ AE;④BO=OE;⑤∠DOE=60°,恒成立的结论有( )
A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC11. 已知∠AOB=30°,点P在∠AOB内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2的形状一定是( )A、直角三角形 B、等边三角形 C、底边和腰不相等的等腰三角形 D、钝角三角形12. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边 DCE,AD与BE交于点O,AD与BC交于点 ,BE与CD交于点Q,连接PQ,以下五个结论:① ACD≌ BCE;②CP=CQ;③PQ AE;④BO=OE;⑤∠DOE=60°,恒成立的结论有( ) A、①②③⑤ B、①③④⑤ C、①②③④ D、①③⑤
A、①②③⑤ B、①③④⑤ C、①②③④ D、①③⑤二、填空题
-
13. 已知在 Rt△ABC 中,∠C=90°,∠A=37°,则∠B=.14. 如图, , ,要使 ,应添加的条件是 . (只需写出一个条件即可)
 15. 如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D,E,若AB=6cm,AC=8cm,BC=10cm,则△ABD的周长为 cm.
15. 如图,在△ABC中,AC的垂直平分线分别交BC、AC于点D,E,若AB=6cm,AC=8cm,BC=10cm,则△ABD的周长为 cm. 16. 点M(-3,m)与点N(n,5)关于x轴对称,则mn =.17. 下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有.(填序号)18. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=30cm,DE=2cm,则BC=cm.
16. 点M(-3,m)与点N(n,5)关于x轴对称,则mn =.17. 下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有.(填序号)18. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=30cm,DE=2cm,则BC=cm.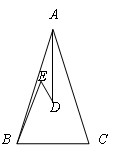
三、解答题
-
19. 化简、求解(1)、若a,b,c是△ABC的三边的长,化简|a-b-c|+|b-c-a|+|c+a-b|.(2)、已知一正多边形的内角与其相邻的外角的比为3:1,求该多边形的边数.20. 如图,已知点A,B(3,﹣2)在平面直角坐标系中,按要求完成下列个小题.

( 1 )写出与点A关于y轴对称的点C的坐标,并在图中描出点C;
( 2 )在(1)的基础上,点B,C表示的是两个村庄,直线a表示河流,现要在河流a上的某点M处修建一个水泵站,向B、C两个村庄供水,并且使得管道BM+CM的长度最短,请你在图中画出水泵站M的位置.
21.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
求证:ABC≌CDE. 22. 在一次数学课上,张老师在屏幕上出示了一个例题:
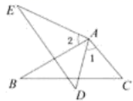
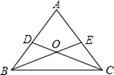
22. 在一次数学课上,张老师在屏幕上出示了一个例题:如图,在△ABC中,D、E分别是AB、AC上的一点,BE与CD交于点O,给出下列四个条件:①BD=CE;②∠BDO=∠CEO;③OB=OC;④∠DBO=∠ECO.要求从这四个等式中选出两个作为已知条件,可判定AB=AC.请写出你的选择,并证明.
 23. 如图,是一个大型模板,设计要求BA与CD相交成26°角,DA与CB相交成37°角,现小燕测得∠A=151°,∠B=66°,∠C=88°,∠D=55°,她就断定这块模板是合格的,这是为什么?
23. 如图,是一个大型模板,设计要求BA与CD相交成26°角,DA与CB相交成37°角,现小燕测得∠A=151°,∠B=66°,∠C=88°,∠D=55°,她就断定这块模板是合格的,这是为什么? 24. 如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.
24. 如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积. 25. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
25. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. (1)、求证:△CEF是等腰三角形;(2)、若CD=3,求DF的长.26. 已知 和 都是等腰直角三角形,点 是直线 上的一动点(点 不与 , 重合),连接 .(1)、在图 中,当点 在边 上时,求证: ;
(1)、求证:△CEF是等腰三角形;(2)、若CD=3,求DF的长.26. 已知 和 都是等腰直角三角形,点 是直线 上的一动点(点 不与 , 重合),连接 .(1)、在图 中,当点 在边 上时,求证: ; (2)、在图 中,当点 在边 的延长线上时,结论 是否还成立?若不成立,请猜想 , , 之间存在的数量关系,并说明理由;
(2)、在图 中,当点 在边 的延长线上时,结论 是否还成立?若不成立,请猜想 , , 之间存在的数量关系,并说明理由; (3)、在图 中,当点 在边 的反向延长线上时,不需写证明过程,直接写出 , , 之间存在的数量关系及直线 与直线 的位置关系.
(3)、在图 中,当点 在边 的反向延长线上时,不需写证明过程,直接写出 , , 之间存在的数量关系及直线 与直线 的位置关系.