广西壮族自治区南宁市隆安县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 以下是四个我国杰出企业代表的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列长度的三条线段为边,能组成三角形的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、4. 下列图形中有稳定性的是( )A、正方形 B、长方形 C、直角三角形 D、平行四边形5. 等腰三角形的一个角是80°,则它的顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°6. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
2. 以下列长度的三条线段为边,能组成三角形的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、4. 下列图形中有稳定性的是( )A、正方形 B、长方形 C、直角三角形 D、平行四边形5. 等腰三角形的一个角是80°,则它的顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°6. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( ) A、SSS B、SAS C、AAS D、ASA7. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、8. 如图,中,是的角平分线, , 交于 , 则的度数是( )
A、SSS B、SAS C、AAS D、ASA7. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、8. 如图,中,是的角平分线, , 交于 , 则的度数是( ) A、 B、 C、 D、9. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A、 B、 C、 D、9. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )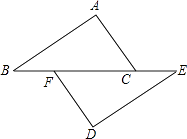 A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC10. 如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为( )
A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC10. 如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为( )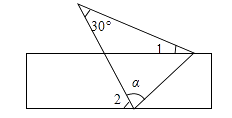 A、 B、 C、 D、11. 小桐把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 等于( )
A、 B、 C、 D、11. 小桐把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 等于( )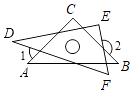 A、 B、 C、 D、12.
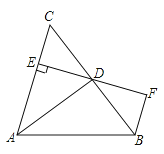
A、 B、 C、 D、12.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 在中,锐角 , 则另一个锐角 .14. 在中, , 则的取值范围是 .15. 已知等腰三角形的一边长等于4,一边长等于5,则它的周长为 .16. 如图,在中,的平分线交于点D.若 , 则点D到边的距离是 .
 17. 如图,已知的周长是23,分别平分和于D,且的面积是 .
17. 如图,已知的周长是23,分别平分和于D,且的面积是 . 18. 如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 .
18. 如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 .
三、解答题
-
19. 如图, 平分 , , ,求 的度数 .
 20. 如图,已知 , , 求证: .
20. 如图,已知 , , 求证: . 21. 证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且 . 求证:点A在的垂直平分线上.
21. 证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且 . 求证:点A在的垂直平分线上. 22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1). (1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点△A1 , B1 , C1的坐标(直接写答案):A1;B1;C1;(3)、求△A1B1C1的面积.23. 已知是的三边长.(1)、若满足, , 试判断的形状;(2)、化简:24. 如图,于于F,若 ,
(1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点△A1 , B1 , C1的坐标(直接写答案):A1;B1;C1;(3)、求△A1B1C1的面积.23. 已知是的三边长.(1)、若满足, , 试判断的形状;(2)、化简:24. 如图,于于F,若 ,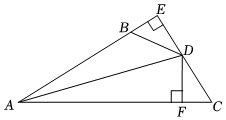 (1)、求证:平分;(2)、已知 , 求的长.
(1)、求证:平分;(2)、已知 , 求的长.


