广西壮族自治区南宁市横县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-12 类型:期中考试
一、单选题
-
1. 中国文字博大精深,而且有许多是轴对称图形,在这四个文字中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列线段能构成三角形的是( )A、2,2,4 B、3,4,5 C、1,2,3 D、2,3,63. 已知 , , , 则的度数为( )A、 B、 C、 D、4. 如图,在中, , , 那么的度数为( )
2. 下列线段能构成三角形的是( )A、2,2,4 B、3,4,5 C、1,2,3 D、2,3,63. 已知 , , , 则的度数为( )A、 B、 C、 D、4. 如图,在中, , , 那么的度数为( ) A、 B、 C、 D、5. 如图,已知平分 , , 判定的理由是( )
A、 B、 C、 D、5. 如图,已知平分 , , 判定的理由是( ) A、 B、 C、 D、6. 如图,在 中, , 平分 ,过点 作 于点 .若 ,则 ( )
A、 B、 C、 D、6. 如图,在 中, , 平分 ,过点 作 于点 .若 ,则 ( ) A、6 B、5 C、4 D、37. 等腰三角形一个角的度数为50°,则顶角的度数为( )A、50° B、80° C、65° D、50°或80°8. 如图,过的顶点A,作边上的高,以下作法正确的是( )
A、6 B、5 C、4 D、37. 等腰三角形一个角的度数为50°,则顶角的度数为( )A、50° B、80° C、65° D、50°或80°8. 如图,过的顶点A,作边上的高,以下作法正确的是( ) A、 B、 C、 D、9. 如图,已知 , , 的延长线交于D,则图中全等的三角形对数是( )
A、 B、 C、 D、9. 如图,已知 , , 的延长线交于D,则图中全等的三角形对数是( ) A、2对 B、3对 C、4对 D、5对10. 如果一个多边形的内角和是720°,那么这个多边形是( )A、六边形 B、五边形 C、四边形 D、三角形11. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
A、2对 B、3对 C、4对 D、5对10. 如果一个多边形的内角和是720°,那么这个多边形是( )A、六边形 B、五边形 C、四边形 D、三角形11. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )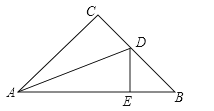 A、4cm B、6cm C、8cm D、10cm12. 等腰三角形一腰上的高与底边所成的角等于( )
A、4cm B、6cm C、8cm D、10cm12. 等腰三角形一腰上的高与底边所成的角等于( )
A、顶角 B、顶角的2倍 C、顶角的一半 D、底角的一半二、填空题
-
13. 已知 , 若的周长为10,则的周长为 .14. 为了防止门框变形常常在门框上钉两根斜拉的木条,这样做的数学依据是三角形的 .15. 已知点P(3,﹣2)与点Q关于x轴对称,则Q点的坐标为 .16. 已知三个内角的度数之比为1∶2∶3,则这三角形最小的内角的度数是 .17. 如图,△ABC是等边三角形,AD⊥BC于点D , AE=AD , 则∠ADE的度数为 .
 18. 如图,等腰的底边的长是 , 面积是 , 腰的垂直平分线交于点N,垂足为M,若D为边上的一动点,P为上的一动点,求的最小值 .
18. 如图,等腰的底边的长是 , 面积是 , 腰的垂直平分线交于点N,垂足为M,若D为边上的一动点,P为上的一动点,求的最小值 .
三、解答题
-
19. 如图,∠1=∠2,∠B=∠D,求证:AB=CD.
 20. 如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形.
20. 如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形. 21. 如图,在△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A,∠C的度数.
21. 如图,在△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A,∠C的度数. 22. 如图,已知 . 求证: .
22. 如图,已知 . 求证: .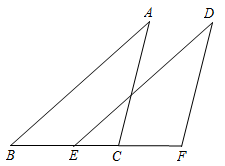 23. 如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠A=∠D.
23. 如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠A=∠D. 24. 如图,已知是等腰直角三角形, , 且于B,于D.
24. 如图,已知是等腰直角三角形, , 且于B,于D. (1)、求证:;(2)、若 , 求 .25. 如图,已知是的外角,是的平分线, , 过的中点H作于F,交于点G.
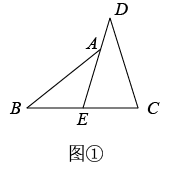
(1)、求证:;(2)、若 , 求 .25. 如图,已知是的外角,是的平分线, , 过的中点H作于F,交于点G. (1)、求证:;(2)、请判断AG与AB的数量关系并说明理由.26. 问题探究:数学课上老师让同学们解决这样的一个问题:如图①,已知E是的中点,点A在上,且 . 求证: .
(1)、求证:;(2)、请判断AG与AB的数量关系并说明理由.26. 问题探究:数学课上老师让同学们解决这样的一个问题:如图①,已知E是的中点,点A在上,且 . 求证: .分析:证明两条线段相等,常用的方法是应用全等三角形或者等腰三角形的性质.本题中要证相等的两条线段不在同一个三角形中,所以考虑从全等三角形入手,而与所在的两个三角形不全等.因此,要证 , 必须添加适当的辅助线构造全等三角形.以下是两位同学添加辅助线的方法.
第一种辅助线做法:如图②,延长到点F,使 , 连接;
第二种辅助线做法:如图③,作于点G,交延长线于点F.

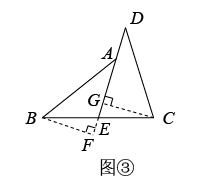
 (1)、请你任意选择其中一种对原题进行证明:
(1)、请你任意选择其中一种对原题进行证明:方法总结:以上方法称之为“倍长中线”法,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线构造全等三角形来解决问题.
(2)、方法运用:如图④,是的中线,与交于点F且 . 求证: .