2022年秋季湘教版数学九年级上册第三章 《图形的相似》单元检测B
试卷更新日期:2022-10-12 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 在△ABC中(如图),点D、E分别为AB、AC的中点,则S△ADE:S△ABC=( )
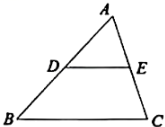 A、1:1 B、1:2 C、1:3 D、1:42. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、1:1 B、1:2 C、1:3 D、1:42. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )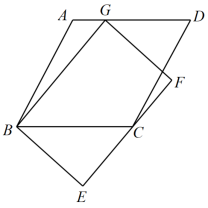 A、 B、 C、 D、33. 如图,相交于点E, , 则的长为( )
A、 B、 C、 D、33. 如图,相交于点E, , 则的长为( ) A、 B、4 C、 D、64. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )
A、 B、4 C、 D、64. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )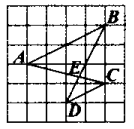 A、1:4 B、4:1 C、1:2 D、2:15. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、1:4 B、4:1 C、1:2 D、2:15. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )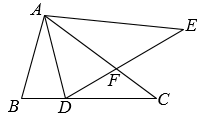 A、①② B、②③ C、①③ D、①②③6. 若 , , ,则 ( )A、 B、 C、 D、7. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
A、①② B、②③ C、①③ D、①②③6. 若 , , ,则 ( )A、 B、 C、 D、7. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( ) A、 B、 C、10 D、8. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、 B、 C、10 D、8. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、189. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、9 B、12 C、15 D、189. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、210. 如图,△ABC与△DEF位似点О为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )
A、 B、1 C、 D、210. 如图,△ABC与△DEF位似点О为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )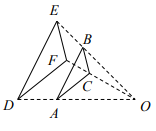 A、4 B、6 C、9 D、16
A、4 B、6 C、9 D、16二、填空题(每题3分,共18分)
-
11. 如图,在矩形中,若 , 则的长为 .
 12. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm.
12. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm. 13. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m.
13. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m. 14. 如图,在中, , 点P为边上任意一点,连接 , 以 , 为邻边作平行四边形 , 连接 , 则长度的最小值为.
14. 如图,在中, , 点P为边上任意一点,连接 , 以 , 为邻边作平行四边形 , 连接 , 则长度的最小值为.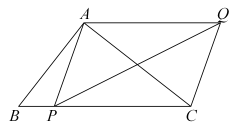 15. 如图,已知菱形的边长为2, , E为的中点,F为的中点,与相交于点G,则的长等于 .
15. 如图,已知菱形的边长为2, , E为的中点,F为的中点,与相交于点G,则的长等于 .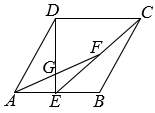 16. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.
16. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.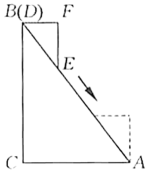
三、解答题(共8题,共72分)
-
17. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.
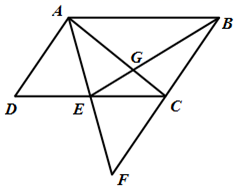 (1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.18. 如图,在 中,点E、F分别在边 、 上,且 .
(1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.18. 如图,在 中,点E、F分别在边 、 上,且 .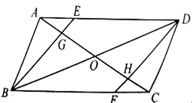 (1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.19. 如图,用四根木条钉成矩形框 ,把边 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
(1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.19. 如图,用四根木条钉成矩形框 ,把边 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).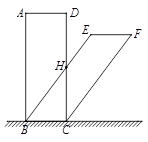 (1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.20. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.
(1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.20. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.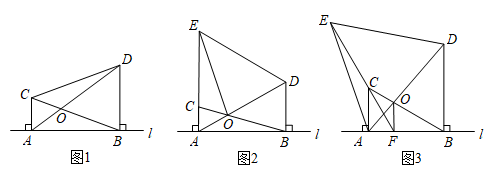 (1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.
(1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.①如图2,当与重合时,连接 , 若 , 求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
21. 综合与实践(1)、问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE,DF分别与边AB,AC交于点M,N,猜想证明:
如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当时,求线段CN的长;
(3)、如图③,在三角板旋转过程中,当AM=AN时,直接写出线段AN的长.22. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .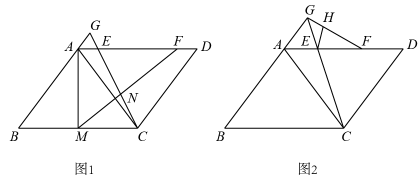 (1)、如图1,是边上一点,连接 , , 与相交于点 .
(1)、如图1,是边上一点,连接 , , 与相交于点 .①若 , 求的长;
②在满足①的条件下,若 , 求证:;
(2)、如图2,连接 , 是上一点,连接 . 若 , 且 , 求的长.23. 已知在 ABC中,O为BC边的中点,连接AO,将 AOC绕点O顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.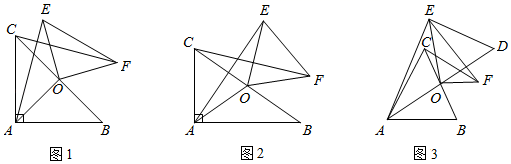 (1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.24. 如图
(1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.24. 如图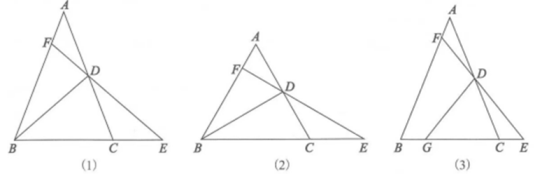
问题提出:如图(1),中, , 是的中点,延长至点 , 使 , 延长交于点 , 探究的值.
(1)、问题探究:
先将问题特殊化.如图(2),当时,直接写出的值;(2)、再探究一般情形.如图(1),证明(1)中的结论仍然成立.(3)、问题拓展:
如图(3),在中, , 是的中点,是边上一点, , 延长至点 , 使 , 延长交于点.直接写出的值(用含的式子表示).