广东省惠州市2022-2023学年九年级上学期数学第一次月考试卷
试卷更新日期:2022-10-12 类型:月考试卷
一、选择题(本大题共10小题,每题3分,共30分)
-
1. 下列函数中,y一定是x的二次函数的是( )A、y=-x2+1 B、y=ax2+bx+c C、 D、x2y=12. 一元二次方程2x2+x-1=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 对于函数 与 的图象的比较,下列说法不正确的是( )A、开口都向下 B、最大值都为0 C、对称轴相同 D、与x轴都只有一个交点4. 用配方法解方程+4x+1=0时,原方程应变形为( )A、 B、 C、 D、5. 学校初二年级组织足球联赛,赛制为单循环制(每两个队之间比赛一场).共进行了28场比赛,问初二年级有几个参赛班级?设初二年级有x个班级参加比赛.根据题意列出方程正确的是( )A、x2=28 B、x(x﹣1)=28 C、x2=28 D、x(x﹣1)=286. 某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共31.若设主干长出 个支干,则所列方程正确的是( )A、 B、 C、 D、7. 已知一元二次方程x2﹣10x+24=0的两个根是菱形的两条对角线长,则这个菱形的面积为( )A、6 B、10 C、12 D、248. 设m,n是一元二次方程x2+2x-7=0的两个根,则m2+3m+n=( )A、5 B、7 C、9 D、119. 已知实数x满足(x2-x)2-4(x2-x)-12=0,则x2-x的值为( )A、6 B、-2或6 C、-2 D、1210. 在同一直角坐标系中,一次函数与二次函数的大致图像可能是( )A、
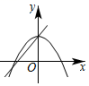 B、
B、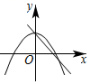 C、
C、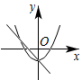 D、
D、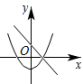
二、填空题(本大题共7题,每题4分,共28分)
-
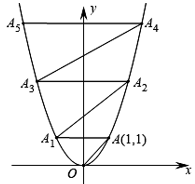
11. 一元二次方程x2=4x的根是 .12. 二次函数 图像的顶点坐标是.13. 若点A(﹣2,y1)和B(1,y2)是二次函数y=-x2﹣k图象上的两点,则y1y2(填“<”“=”或“>”).14. 若一元二次方程x2+2x﹣3=0的两根为x1 , x2 , 则x12+x22= .15. 有一种流感病毒,刚开始有2人患了流感,经过两轮传染后共有128人患流感,如果设每轮传染中一个人平均传染x个人,那么可列方程为 .16. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.17. 在平面直角坐标系中,抛物线 的图象如图所示.已知A点坐标为 ,过点A作 轴交抛物线于点 ,过点 作 交抛物线于点 ,过点 作 轴交抛物线于点 ,过点 作 交抛物线于点 …,依次进行下去,则点 的坐标为 .
三、解答题(一)(本大题共3题,每题6分,共18分)
-
18. 用合适的方法解下列方程:(1)、(2)、 .19. 已知一元二次方程的一个根是1.求的值和方程的另一个根.20. 抛物线y=ax2+c与y=-5x2的形状、开口方向都相同,且y=ax2+c经过(0,3).求:(1)、该抛物线的解析式;(2)、y=ax2+c是由抛物线y=-5x2经过怎样的平移得到的?
四、解答题(二)(本大题共3题,每题8分,共24分)
-
21. 某口罩生产厂生产的口罩1月份平均日产量为30000个,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,厂决定从2月份起扩大产量,3月份平均日产量达到36300个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?22. 如图,某农户准备建一个长方形养鸡场ABCD,养鸡场的一边靠墙,另三边用篱笆围成,若墙长为18 m,墙对面有一个2 m宽的门,篱笆总长为33 m,围成的长方形养鸡场除门之外四周不能有空隙.
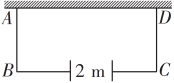 (1)、若AB=x m,则BC=m;(2)、要使围成的养鸡场面积为150 m2 , 则AB的长为多少?23. 已知关于x的方程x2﹣2(m+1)x+m2+2=0.(1)、若方程总有两个实数根,求m的取值范围;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=8,求m的值.
(1)、若AB=x m,则BC=m;(2)、要使围成的养鸡场面积为150 m2 , 则AB的长为多少?23. 已知关于x的方程x2﹣2(m+1)x+m2+2=0.(1)、若方程总有两个实数根,求m的取值范围;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=8,求m的值.五、解答题(三)(本大题共2题,每题10分,共20分)
-
24. 某超市经销一种商品,每千克成本为30元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的四组对应值如下表所示:
销售单价x(元/千克)
40
45
55
60
销售量y(千克)
80
70
50
40
(1)、求y与x之间的函数表达式;(2)、若商店按不低于成本价,且不高于60元的单价销售该商品,要使每天获得的利润为800元,求每天的销售量;(3)、能使销售该商品每天获得的利润为1400元吗?若能,销售单价为多少?若不能,请说明理由.25. 已知,点 , 点和抛物线 , 将抛物线沿着轴方向平移经过点 , 画出平移后的抛物线如图所示.
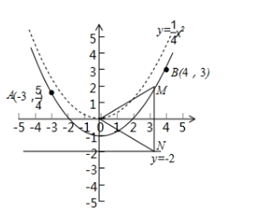 (1)、平移后的抛物线是否经过点 ?说明你的理由;(2)、在平移后的抛物线上且位于直线下方的图像上是否存在点 , 使?若存在,请求出点的坐标;若不存在,请说明理由;(3)、在平移后的抛物线上有点 , 过点作直线的垂线,垂足为 , 连接 , 当时,直接写出的坐标.
(1)、平移后的抛物线是否经过点 ?说明你的理由;(2)、在平移后的抛物线上且位于直线下方的图像上是否存在点 , 使?若存在,请求出点的坐标;若不存在,请说明理由;(3)、在平移后的抛物线上有点 , 过点作直线的垂线,垂足为 , 连接 , 当时,直接写出的坐标.