2022年秋季湘教版数学九年级上传第三章 《图形的相似》单元检测A
试卷更新日期:2022-10-12 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、162. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( )
 A、9cm B、12cm C、15cm D、18cm3. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )
A、9cm B、12cm C、15cm D、18cm3. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )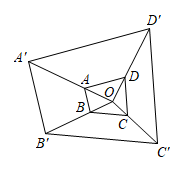 A、4 B、6 C、16 D、184. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、4 B、6 C、16 D、184. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )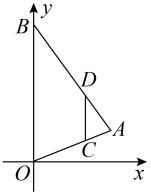 A、4 B、5 C、6 D、76. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A、4 B、5 C、6 D、76. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( ) A、5 B、6 C、 D、7. 如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( )
A、5 B、6 C、 D、7. 如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( ) A、 B、 C、 D、8. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( )
A、 B、 C、 D、8. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( ) A、 B、 C、 D、9. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、 B、 C、 D、9. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、 B、 C、1 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每题3分,共18分)
-
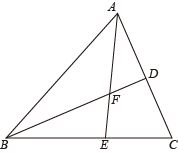
11. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=3 , 则△ABC的周长为 .
 12. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .
12. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .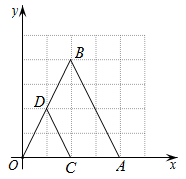 13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .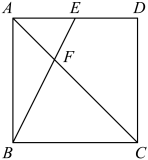 14. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .
14. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .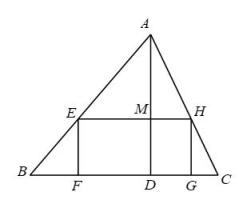 15. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
15. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.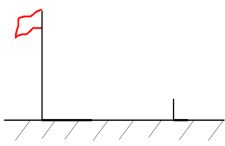 16. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.
16. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.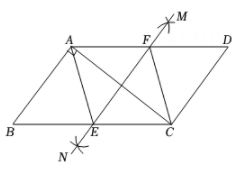
三、解答题(共8题,共72分)
-
17. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .
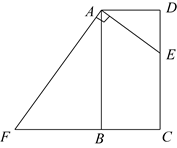 (1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.18. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.18. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.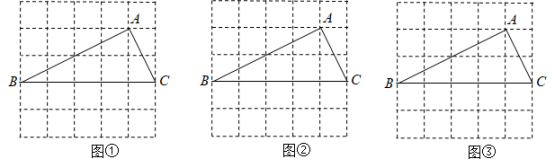 (1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.19. 如图,四边形为菱形,点E在的延长线上, .
(1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.19. 如图,四边形为菱形,点E在的延长线上, . (1)、求证:;(2)、当时,求的长.20. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形, 、
(1)、求证:;(2)、当时,求的长.20. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形, 、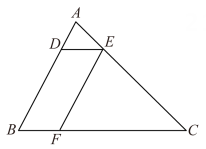 (1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.21. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证:
(1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.21. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证: (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ22. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ22. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE. (1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.
(1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为 ▲ ;
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.
23. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线 , 与的面积相等吗?为什么?
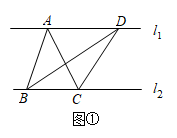
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .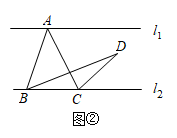
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .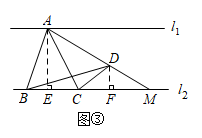
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .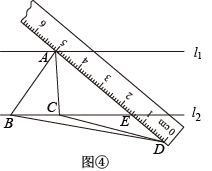 24. 华师版八年级下册数学教材第121页习题19.3第2小题及参考答案.
24. 华师版八年级下册数学教材第121页习题19.3第2小题及参考答案.2.如图,在正方形ABCD中,.求证:.
证明:设CE与DF交于点O,
∵四边形ABCD是正方形,
∴ , .
∴.
∵ ,
∴.
∴.
∴.
∴.
∴.
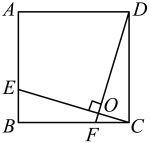
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究
(1)、【问题探究】如图,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DA上,且.试猜想的值,并证明你的猜想. (2)、【知识迁移】如图,在矩形ABCD中, , , 点E、F、G、H分别在线段AB、BC、CD、DA上,且.则.
(2)、【知识迁移】如图,在矩形ABCD中, , , 点E、F、G、H分别在线段AB、BC、CD、DA上,且.则. (3)、【拓展应用】如图,在四边形ABCD中, , , , 点E、F分别在线段AB、AD上,且.求的值.
(3)、【拓展应用】如图,在四边形ABCD中, , , , 点E、F分别在线段AB、AD上,且.求的值.