河南省豫北名校2022-2023学年高二上学期数学9月教学质量检测试卷
试卷更新日期:2022-10-11 类型:月考试卷
一、单选题
-
1. 已知向量 , 则的值为( )A、 B、21 C、 D、42. 直线的倾斜角为( )A、 B、 C、 D、3. 已知圆的一般方程为 , 其圆心坐标是( )A、 B、 C、 D、4. 与向量反向的单位向量的坐标为( )A、 B、 C、 D、5. 已知直线 , , 若 , 则实数的值为( )A、1 B、 C、 D、6. 圆与圆的位置关系是( )A、内切 B、相交 C、外切 D、相离7. 已知圆关于直线(a,b为大于0的数)对称,则的最小值为( )A、 B、 C、1 D、28. 已知向量 , 的夹角为锐角,则实数的取值范围为( )A、 B、 C、 D、9. 如图,直三棱柱底面是直角三角形,且 , E,F,G分别为 , , 的中点,则EF与平面所成角的正弦值为( )
 A、 B、 C、 D、10. 已知点 , , 点关于直线的对称点为点 , 在中, , 则面积的最大值为( )
A、 B、 C、 D、10. 已知点 , , 点关于直线的对称点为点 , 在中, , 则面积的最大值为( ) A、 B、 C、 D、11. 如图,在平行六面体中,底面是边长为2的正方形.若 , 且 , 则的长为( )
A、 B、 C、 D、11. 如图,在平行六面体中,底面是边长为2的正方形.若 , 且 , 则的长为( )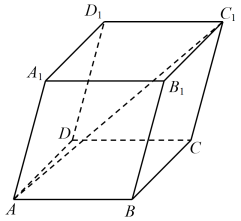 A、 B、 C、 D、512. 若直线与曲线有两个不同的交点,则实数的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、512. 若直线与曲线有两个不同的交点,则实数的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 直线 , 的斜率 , 是关于的方程的两根,若 , 则实数 .14. 已知 , , , 点 , 若平面ABC,则点的坐标为 .15. 若圆上恰有2个点到直线的距离为2,则实数的取值范围为 .16. 如图,已知正方体的棱长为4, , , 分别是棱 , , 的中点,设是该正方体表面上的一点,若 , 则点的轨迹围成图形的面积是;的最大值为 .

三、解答题
-
17. 已知直线 , , .(1)、若这三条直线交于一点,求实数的值;(2)、若三条直线能构成三角形,求满足的条件.18. 如图,在四棱锥中,底面ABCD为矩形,平面PAD,E是AD的中点,为等腰直角三角形, , .
 (1)、求证:;(2)、求PC与平面PBE所成角的正弦值.
(1)、求证:;(2)、求PC与平面PBE所成角的正弦值. 19. 已知圆的方程为 .(1)、求实数的取值范围;(2)、若圆与直线交于M,N两点,且 , 求的值.20. 在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,且满足(如图1),将沿EF折起到的位置,使二面角成直二面角,连接 , (如图2).
19. 已知圆的方程为 .(1)、求实数的取值范围;(2)、若圆与直线交于M,N两点,且 , 求的值.20. 在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,且满足(如图1),将沿EF折起到的位置,使二面角成直二面角,连接 , (如图2). (1)、求证:;(2)、求二面角的正弦值.
(1)、求证:;(2)、求二面角的正弦值.
