湖北省部分重点中学2022-2023学年高二上学期数学9月联考试卷
试卷更新日期:2022-10-11 类型:月考试卷
一、单选题
-
1. 已知向量与的夹角是 , 且 , 若 , 则实数( )A、 B、 C、-2 D、22. 若复数z满足 , 则z的虚部为( )A、 B、 C、 D、3. 已知 , , 表示直线, 表示平面,给出下列命题:
①若 , ,那么 ;②若 , ,那么 ;③若 , ,则 ;④若 , ,那么 .其中正确的命题个数是( )
A、0 B、1 C、2 D、34. 《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体,如图,羡除ABCDEF中,底面ABCD是正方形,平面ABCD, , 其余棱长都为1,则这个几何体的外接球的体积为( )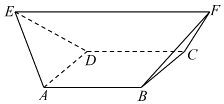 A、 B、 C、 D、5. 某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A、 B、 C、 D、5. 某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( ) A、这五个社团的总人数为100 B、脱口秀社团的人数占五个社团总人数的20% C、这五个社团总人数占该校学生人数的8% D、从这五个社团中任选一人,其来脱口秀社团或舞蹈社团的概率为50%6. 已知平面上三点坐标为、、 , 小明在点处休息,一只小狗沿所在直线来回跑动,则小狗距离小明最近时所在位置的坐标为( )A、 B、 C、 D、7. 高一年级某同学为了丰富自己的课外活动,参加了学校“文学社”“咏春社”“音乐社”三个社团的选拔,该同学能否成功进入这三个社团是相互独立.假设该同学能够进入“文学社”“咏春社”“音乐社”三个社团的概率分别为、、 , 该同学可以进入两个社团的概率为 , 且三个社团都进不了的概率为 , 则( )A、 B、 C、 D、8. 在中, , , , 为线段上的动点,且 , 则的最小值为( )A、 B、 C、 D、
A、这五个社团的总人数为100 B、脱口秀社团的人数占五个社团总人数的20% C、这五个社团总人数占该校学生人数的8% D、从这五个社团中任选一人,其来脱口秀社团或舞蹈社团的概率为50%6. 已知平面上三点坐标为、、 , 小明在点处休息,一只小狗沿所在直线来回跑动,则小狗距离小明最近时所在位置的坐标为( )A、 B、 C、 D、7. 高一年级某同学为了丰富自己的课外活动,参加了学校“文学社”“咏春社”“音乐社”三个社团的选拔,该同学能否成功进入这三个社团是相互独立.假设该同学能够进入“文学社”“咏春社”“音乐社”三个社团的概率分别为、、 , 该同学可以进入两个社团的概率为 , 且三个社团都进不了的概率为 , 则( )A、 B、 C、 D、8. 在中, , , , 为线段上的动点,且 , 则的最小值为( )A、 B、 C、 D、二、多选题
-
9. 下列结论正确的是( )A、若 , 互为对立事件, , 则 B、若事件 , , 两两互斥,则事件与互斥 C、若事件与对立,则 D、若事件与互斥,则它们的对立事件也互斥10. 下列说法中错误的为( )A、已知 , 且与的夹角为锐角,则实数的取值范围是 B、向量 , 不能作为平面内所有向量的一组基底 C、非零向量 , , 满足且与同向,则 D、非零向量和 , 满足 , 则与的夹角为11. 在棱长为的正方体中,点P在正方形内含边界运动,则下列结论正确的是( ).A、若点P在上运动,则 B、若平面 , 则点P在上运动 C、存在点P,使得平面PBD截该正方体的截面是五边形 D、若 , 则四棱锥的体积最大值为112. 已知 , 是圆O:上两点,则下列结论正确的是( )A、若 , 则 B、若点O到直线AB的距离为 , 则 C、若 , 则的最大值为 D、若 , 则的最大值为4
三、填空题
-
13. 向量在向量方向上的投影向量的坐标为.14. 定义一个新的运算: . 若复数z使 , 则 .15. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位临湘市居民,他们的幸福感指数为 3,4,5,5,6,7,7,8,9,10.则这组数据的 80%分位数是.16. 如图,四棱锥的底面是菱形,其对角线 , , 、都与平面垂直, , . 则三棱锥与四棱锥公共部分的体积是 .

四、解答题
-
17. 已知在△ABC中,角A,B,C的对边分别为a,b,c,____.
①;②;③ .
请在以上三个条件中任选一个补充在横线处,并解答:
(1)、求角C的值;(2)、若且 , 求的值.18. 过点作直线分别交轴正半轴于两点 (1)、当面积最小时,求直线的方程;(2)、当取最小值时,求直线的方程
(1)、当面积最小时,求直线的方程;(2)、当取最小值时,求直线的方程 19. 已知的斜边为 , 且.求:(1)、直角顶点的轨迹方程;(2)、直角边的中点的轨迹方程.20. 为打造精品赛事,某市举办“南粤古驿道定向大赛”,该赛事体现了“体育+文化+旅游”全方位融合发展.本次大赛分少年组、成年组、专业组三个小组,现由工作人员统计各个组别的参赛人数以及选手们比赛时的速度,得到如下统计表和频率分布直方图:
19. 已知的斜边为 , 且.求:(1)、直角顶点的轨迹方程;(2)、直角边的中点的轨迹方程.20. 为打造精品赛事,某市举办“南粤古驿道定向大赛”,该赛事体现了“体育+文化+旅游”全方位融合发展.本次大赛分少年组、成年组、专业组三个小组,现由工作人员统计各个组别的参赛人数以及选手们比赛时的速度,得到如下统计表和频率分布直方图:组数
速度(千米/小时)
参赛人数(单位:人)
少年组
300
成年组
600
专业组
 (1)、求a , b的值;(2)、估计本次大赛所有选手的平均速度(同一组数据用该组数据的中间值作代表,最终计算结果精确到0.01);(3)、通过分层抽样从成年组和专业组中抽取6人,再从这6人中随机抽取2人接受采访,求接受采访的2人都来自“成年组”的概率.21. 如图,在四棱锥中,底面是矩形, , , 平面 , 且是PD的中点.
(1)、求a , b的值;(2)、估计本次大赛所有选手的平均速度(同一组数据用该组数据的中间值作代表,最终计算结果精确到0.01);(3)、通过分层抽样从成年组和专业组中抽取6人,再从这6人中随机抽取2人接受采访,求接受采访的2人都来自“成年组”的概率.21. 如图,在四棱锥中,底面是矩形, , , 平面 , 且是PD的中点. (1)、求证:平面;(2)、求异面直线与所成角的正切值;(3)、求平面与平面所成的夹角的大小.22. 在2021年6月17日,神舟十二号载人飞船顺利升空并于6.5小时后与天和核心舱成功对接.如图,是神舟十二号飞船推进舱及其推进器的简化示意图,半径相等的圆 , , , , 与圆柱底面相切于A, , , 四点,且圆与 , 与 , 与 , 与分别外切,线段为圆柱的母线.点线段中点,点在线段上,且 . 已知圆柱 , 底面半径为2,.
(1)、求证:平面;(2)、求异面直线与所成角的正切值;(3)、求平面与平面所成的夹角的大小.22. 在2021年6月17日,神舟十二号载人飞船顺利升空并于6.5小时后与天和核心舱成功对接.如图,是神舟十二号飞船推进舱及其推进器的简化示意图,半径相等的圆 , , , , 与圆柱底面相切于A, , , 四点,且圆与 , 与 , 与 , 与分别外切,线段为圆柱的母线.点线段中点,点在线段上,且 . 已知圆柱 , 底面半径为2,.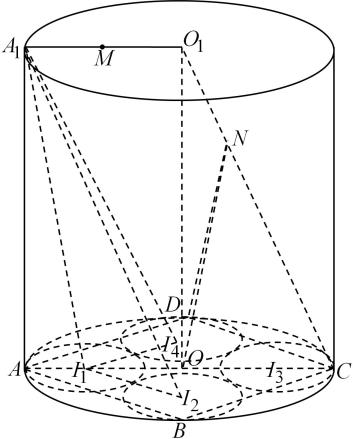
 (1)、求证:平面;(2)、线段上是否存在一点 , 使得平面?若存在,请求出的长,若不存在,请说明理由;(3)、如图,是飞船推进舱与即将对接的天和核心舱的相对位置的简化示意图.天和核心舱为底面半径为2的圆柱 , 它与飞船推进舱共轴,即 , , , 共线.核心舱体两侧伸展出太阳翼,其中三角形为以为斜边的等腰直角三角形,四边形为矩形.已知推进舱与核心舱的距离为4,即 , 且 , . 在对接过程中,核心舱相对于推进舱可能会相对作出逆时针旋转的运动,请你求出在舱体相对距持不变的情况下,在舱体相对旋转过程中,直线与平面所成角的正弦值的最大值.
(1)、求证:平面;(2)、线段上是否存在一点 , 使得平面?若存在,请求出的长,若不存在,请说明理由;(3)、如图,是飞船推进舱与即将对接的天和核心舱的相对位置的简化示意图.天和核心舱为底面半径为2的圆柱 , 它与飞船推进舱共轴,即 , , , 共线.核心舱体两侧伸展出太阳翼,其中三角形为以为斜边的等腰直角三角形,四边形为矩形.已知推进舱与核心舱的距离为4,即 , 且 , . 在对接过程中,核心舱相对于推进舱可能会相对作出逆时针旋转的运动,请你求出在舱体相对距持不变的情况下,在舱体相对旋转过程中,直线与平面所成角的正弦值的最大值.