吉林省长春市榆树市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{8}$ B、 $- \sqrt{3}$ C、 $\sqrt{12}$ D、 $\sqrt{48}$

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、明天的最高气温将达35℃ B、任意购买一张动车票，座位刚好挨着窗口 C、掷两次质地均匀的骰子，其中有一次正面朝上 D、对顶角相等

查看试题解析
3. 如图，在ABC中，D，E分别是AB，AC上的点，且DE// BC，若AE： EC=1： 4，那么 $S_{△ A D E} ： S_{△ B E C}$ 的值为（）

A、1∶16 B、1∶18 C、1∶20 D、1∶24

查看试题解析
4. 如图，在Rt△ABC中，CE是斜边AB上的中线，CD⊥AB ，若CD＝5，CE＝6，则△ABC的面积是（）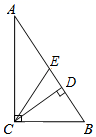

A、24 B、25 C、30 D、36

查看试题解析
5. 一元二次方程x²﹣3x+5=0的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、只有一个实数根 D、有两个不相等的实数根

查看试题解析
6. 如图，河坝横断面迎水坡 $A B$ 的坡比为 $1$ ： $\sqrt{3}$ ，坝高 $B C = 3$ m，则 $A B$ 的长度为（）

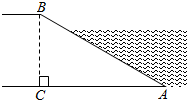A、6m B、 $3 \sqrt{3}$ m C、9m D、 $6 \sqrt{3}$ m

查看试题解析
7. 如图，某停车场人口的栏杆，从水平位置AB绕点O旋转到A'B′的位置已知AO＝4m ，若栏杆的旋转角∠AOA′＝50°时，栏杆A端升高的高度是（）

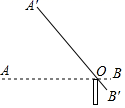A、 $\frac{4}{\sin 50^{°}}$ B、4sin50° C、 $\frac{4}{\cos 50^{°}}$ D、4cos50°

查看试题解析
8. 对于二次函数y＝﹣2x² ，下列结论正确的是（）

A、y随x的增大而增大 B、图象关于直线x＝0对称 C、图象开口向上 D、无论x取何值，y的值总是负数

查看试题解析

二、填空题

9. 计算：tan²45°+1＝．

查看试题解析
10. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
11. 若关于x的一元二次方程 $x^{2} + 2 x - k = 0$ 的一个根为1，则k的值为．

查看试题解析
12. 抛物线 $y = \frac{1}{2} {(x - 2)}^{2}$ 的顶点坐标是．

查看试题解析
13. 一只蚂蚁在如图所示的方格地板上随机爬行，每个小方格形状大小完全相同，当蚂蚁停下时，停在地板中阴影部分的概率为．

查看试题解析
14. 我市某公司前年缴税40万元，今年缴税48.4万元．该公司缴税的年平均增长率为．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} - \sqrt{18} + 3 \sqrt{\frac{1}{3}} + \sqrt{8}$ ．

查看试题解析
16. 解方程：x²＋4x＋1＝0.

查看试题解析
17. 有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，3；乙袋中有2个球，分别标有数字1，4，这5个球除所标数字不同外其余均相同．从甲、乙两袋中各随机摸出1个球．用画树状图（或列表）的方法，求摸出的两个球上数字之和是4的概率．

查看试题解析
18. 如图，在一个长10cm，宽6cm的矩形铁皮的四角各截去一个同样的小正方形，然后折叠成一个无盖的长方形盒子．若长方形盒子的底面（图中阴影部分）面积是32cm² ，求截去的小正方形的边长．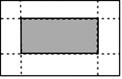

查看试题解析
19. 如图，航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°，此时航拍无人机A处与该建筑物的水平距离AD为80米．求该建筑物的高度BC（精确到1米）．（参考数据：sin65°＝0.91，cos65°＝0.42，tan65°＝2.14）

查看试题解析
20. 若抛物线y＝ax²+bx﹣3的对称轴为直线x＝1，且该抛物线经过点（3，0）．

(1)、求该抛物线对应的函数表达式．

(2)、当﹣2≤x≤2时，则函数值y的取值范围为．

(3)、若方程ax²+bx﹣3＝n有实数根，则n的取值范围为．

查看试题解析
21. 如图，在6×8的网格图中，每个小正方形边长均为1，原点O和 $△ A B C$ 的顶点均为格点．

(1)、以O为位似中心，在网格图中作 $△ A^{'} B^{'} C^{'}$ ，使 $△ A^{'} B^{'} C^{'}$ 与 $△ A B C$ 位似，且位似比为1：2．（保留作图痕迹，不要求写作法和证明）

(2)、若点C的坐标为 $(2 ， 4)$ ，则 $A^{^{'}} B^{^{'}} =$ ， $△ A^{'} B^{'} C^{'}$ 的面积＝．

查看试题解析
22. 在矩形 $A B C D$ 中，E为边 $C D$ 上一点，把 $△ A D E$ 沿 $A E$ 翻折，使点D恰好落在边 $B C$ 上的点F处．

(1)、求证： $△ A B F ∽ △ F C E$ ．

(2)、若 $A D = 10$ ， $C D = 6$ ，则 $\tan ∠ E A F$ 的值为．

(3)、若 $A D = 6$ ， $D E = 3$ ，则AB的长为．

查看试题解析
23. 如图，在平面直角坐标系中，抛物线y＝ $\frac{1}{2}$ （x﹣1）²﹣2与x轴交于点A和点B（点A在点B的左侧），第一象限内的点C在该抛物线上．

(1)、直接写出A、B两点的坐标；

(2)、若 $△ A B C$ 的面积为12，求点C坐标；

(3)、在（2）问的条件下，直线y＝mx+n经过点A、C， $\frac{1}{2}$ （x﹣1）²﹣2＞mx+n时，直接写出x的取值范围．

查看试题解析
24. 如图，在矩形ABCD中，AB=6，BC=8，点O为对角线AC的中点，动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，点P运动速度为每秒2个单位长度，点Q运动速度为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止运动，连结PQ，设点P运动时间为t（t＞0）秒．

(1)、cos∠BAC= ．

(2)、当PQ⊥AC时，求t的值．

(3)、求△QOP的面积S关于t的函数表达式，并写出t的取值范围．

(4)、当线段PQ的垂直平分线经过△ABC的某个顶点时，请直接写出t的值．

查看试题解析