吉林省长春市新区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 化简二次根式 的符合题意结果是( )A、3 B、 C、 D、2. 下列方程中,是关于x的一元二次方程的是( )A、 B、2x2﹣x=1 C、3x3=1 D、xy=43. 若 = ,则 的值为( )A、5 B、 C、3 D、4. 有5张完全相同的卡片,正面分别写有1,2,3,4,5这5个数字,现把卡片背面朝上,从中随机抽取一张卡片,其数字是奇数的概率为( )A、 B、 C、 D、5. 根据下列表格中的对应值,判断方程( , a,b,c为常数)的根的个数是( )
6.17
6.18
6.19
6.20
0.02
-0.01
0.02
0.04
A、0 B、1 C、2 D、1或26. 在Rt△ABC中,∠C=90°,AB=2BC,那么sinA的值为( )
A、 B、 C、 D、17.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
 A、
A、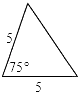 B、
B、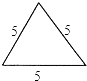 C、
C、 D、
D、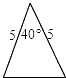 8. 在平面直角坐标系中,若函数的图象与坐标轴共有三个交点,则下列各数中可能的值为( )A、-1 B、0 C、1 D、2
8. 在平面直角坐标系中,若函数的图象与坐标轴共有三个交点,则下列各数中可能的值为( )A、-1 B、0 C、1 D、2二、填空题
-
9. 计算sin60°+tan30°= .10. 若关于x的方程x2+(m2﹣2)x﹣15=0有一个根是x=3,则m的值是 .11. 已知二次函数 ,当 时,y随着x的增大而减小,请写出一个符合条件的m的值是.12. 某市某楼盘准备以每平方米7200元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米5832元的均价开盘销售.则平均每次下调的百分率为 .13. 如图,一抛物线型拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1.5米后,水面的宽度为 米.
 14. 如图,在2×4的方格中,两条线段的夹角(锐角)为∠1,则sin∠1=.
14. 如图,在2×4的方格中,两条线段的夹角(锐角)为∠1,则sin∠1=.
三、解答题
-
15. 解方程:x2+2x﹣2=0.16. 先化简,再求值:6x2+2xy﹣8y2﹣2(3xy﹣4y2+3x2),其中x= ,y= .17. 某校围棋队共有4名队员,分别是:小明、小红、小聪、小丽,其中小明、小红来自八年级,小聪、小丽来自九年级,现准备抽取两名队员参加集训.(1)、若从八年级、九年级中各随机抽取一人,则小红和小丽恰好被抽到参加集训的概率为 ;(2)、若从四名队员中随机抽取两名队员,请用列表法或画树状图法求抽到小明和小聪的概率.18. 在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图
 (1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.
(1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.(①只能用无刻度的直尺作直线;②保留作图痕迹)
19. 全球最长跨海大桥——港珠澳大桥连接香港、澳门、珠海三地,总长55千米.大桥某段采用低塔斜拉桥桥型,图2是从图1引申出的平面图.假设你站在桥上测得拉索与水平桥面的夹角是 , 拉索与水平桥面的夹角是 , 两拉索顶端的距离为2米,两拉索底端距离为20米,请求出立柱的长.(结果精确到0.1米,). 20. 如图,有一道长为的墙,计划用总长为的栅栏,靠墙围成由三个小长方形组成的矩形花圃 . 若花圃的面积为 , 求的长.
20. 如图,有一道长为的墙,计划用总长为的栅栏,靠墙围成由三个小长方形组成的矩形花圃 . 若花圃的面积为 , 求的长. 21. 已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)、证明:不论m为何值时,方程总有实数根;(2)、m为何整数时,方程有两个不相等的正整数根.22. 如图,AD、BE是△ABC的高,连接DE.
21. 已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)、证明:不论m为何值时,方程总有实数根;(2)、m为何整数时,方程有两个不相等的正整数根.22. 如图,AD、BE是△ABC的高,连接DE. (1)、求证:△ACD∽△BCE;(2)、若点D是BC的中点,CE=6,BE=8,求AB的长.23. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止运动,设运动时间为t秒.
(1)、求证:△ACD∽△BCE;(2)、若点D是BC的中点,CE=6,BE=8,求AB的长.23. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止运动,设运动时间为t秒. (1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;(3)、当t为何值时,△CPQ与△CAD相似?请直接写出t的值.24. 已知二次函数y=ax2﹣2ax﹣2(a≠0).(1)、该二次函数图象的对称轴是直线 ;(2)、若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为 , 求点M和点N的坐标;(3)、已知线段PQ的两个端点坐标分别为P(0,﹣4)、Q(3,﹣4),当此函数图象与线段PQ只有一个交点时,直接写出a的取值范围.(4)、对于该二次函数图象上的两点A(x1 , y1)、B(x2 , y2),当x2≥3时,y1≥y2恒成立,设t≤x1≤t+1,请结合图象,直接写出t的取值范围
(1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;(3)、当t为何值时,△CPQ与△CAD相似?请直接写出t的值.24. 已知二次函数y=ax2﹣2ax﹣2(a≠0).(1)、该二次函数图象的对称轴是直线 ;(2)、若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为 , 求点M和点N的坐标;(3)、已知线段PQ的两个端点坐标分别为P(0,﹣4)、Q(3,﹣4),当此函数图象与线段PQ只有一个交点时,直接写出a的取值范围.(4)、对于该二次函数图象上的两点A(x1 , y1)、B(x2 , y2),当x2≥3时,y1≥y2恒成立,设t≤x1≤t+1,请结合图象,直接写出t的取值范围