吉林省通化市梅河口市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，属于一元二次方程的是（）

A、2x﹣2＝3 B、x²＝2x C、x+y＝2 D、 $\frac{1}{x}$ +x＝3

查看试题解析
2. 下面图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一个不透明的袋子中装有1个红球，2个白球，这3个球除颜色外完全相同，现从中随机抽取1个球，下列事件属于必然事件的是（）

A、抽到的是红球 B、抽到的是白球 C、抽到的是黑球 D、抽到的是红球或白球

查看试题解析
4. 下列各点中，在反比例函数y＝﹣ $\frac{4}{x}$ 图象上的是（）

A、（﹣1，4） B、（1，4） C、（﹣2，﹣2） D、（2，2）

查看试题解析
5. 如图所示的正六边形花环绕中必至少旋转 $α$ 度能与自身重合，则 $α$ 为（）

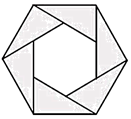A、30 B、60 C、120 D、180

查看试题解析
6. 如图，在平面直角坐标系中，点A的坐标为(﹣1，2)，以点O为圆心，将线段OA逆时针旋转，使点A落在x轴的负半轴上点B处，则点B的横坐标为（）

A、﹣ $\sqrt{3}$ B、 $\sqrt{3}$ C、﹣ $\sqrt{5}$ D、 $\sqrt{5}$

查看试题解析

二、填空题

7. 某班级有男生30名，女生20名，从该班随机找一名学生是女生的概率为．

查看试题解析
8. 若关于x的一元二次方程x²﹣2x+m＝0有两个相等的实数根，则实数m的值为.

查看试题解析
9. 已知二次函数y＝x²+6x+c（c为常数）的图象与x轴的一个交点为(﹣1，0)，则它与x轴的另一个交点的坐标是．

查看试题解析
10. 如图，正六边形ABCDEF内接于⊙O，连接OC、OD，若OC长为2cm，则正六形ABCDEF的周长为cm．

查看试题解析
11. 如图，点A、B、C在⊙O上，∠ACB+∠AOB=90°，则∠ACB的大小为

查看试题解析
12. 在一个不透明的盒子里装有质地大小都相同的红球和黑球共4个，将球搅后从中随机摸出一个记下颜色，放回，再重复进行下一次试验，如表是他们整理得到的．试验数据：
摸球的次数n
500
1000
2000
2500
3000
5000
摸到红球的次数m
351
722
1486
1870
2262
3760
摸到红球的频率 $\frac{m}{n}$
0.702
0.722
0.743
0.748
0.754
0.752
根据上表估计在盒子中随机摸出一个球是红球的概率为．（精确到0.01）

查看试题解析
13. 如图，菱形OABC在第一象限内，∠AOC＝60°，反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象经过点A，交BC边于点D，若△AOD的面积为 $\sqrt{3}$ ，则k的值为．

查看试题解析
14. 二次函数y＝ax²+bx+c图像上部分点的坐标满足下表：
x
…
﹣1
1
2
3
4
…
y
…
﹣6
﹣2
﹣3
﹣6
﹣11
…
则不等式ax²+bx+c＞﹣3的解集为．

查看试题解析
15. 如图，在平面直角坐标系中， $A (0 ， 4)$ 、 $B (2 ， 4)$ 、 $C (4 ， 2)$ ．

(1)、经过 $A$ 、 $B$ 、 $C$ 三点的圆弧所在圆的圆心 $M$ 的坐标为；

(2)、这个圆的半径为；

(3)、点 $D (3 ， - 1)$ 与 $⊙ M$ 的位置关系为点 $D$ 在 $⊙ M$ （填内、外、上）．

查看试题解析

三、解答题

16. 解方程：x²﹣4x+2＝0．

查看试题解析
17. 如图，在7×7的正方形网格中，每个小正方形的边长都是1个单位长度，每个小正方形的顶点称为格点， $△ A B C$ 的顶点均在格点上．将 $△ A B C$ 绕点 $C$ 顺时针旋转 $90 °$ ，得到 $△ D E C$ ．

(1)、画出 $△ D E C$ ；

(2)、边 $A C$ 在旋转过程中扫过的图形面积为．

查看试题解析
18. 如图，某课外活动小组利用一面墙（墙足够长），另三边用20m长的篱笆围成一个面积为 $50 m^{2}$ 的矩形花园ABCD，求边AB的长．

查看试题解析
19. 在平面直角坐标系中，抛物线y＝x²+bx+c经过点(﹣1，9)、(2，﹣3)．

(1)、求这条抛物线所对应的函数表达式；

(2)、点P是这条抛物线上一点，其横、纵坐标互为相反数，求点P的坐标．

查看试题解析
20. 在一个不透明的袋子里装有除数字外完全相同的3个小球，上面分别标有数字2，3，4．甲、乙两名同学做摸球游戏，游戏规则是：甲先从袋中随机摸出一个小球，乙再从袋中剩下的2个小球中随机摸出一个小球．若摸出的两个小球上的数字和为偶数，则甲胜，否则乙胜．

(1)、用列表法或画树状图法，求甲胜的概率；

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析
21. 如图，在平面直角坐标系中，直线y＝kx+b（k≠0）与双曲线y＝ $\frac{m}{x}$ （m≠0）交于点A(2，﹣3)和点B(n，2)．

(1)、分别求直线与双曲线对应的函数表达式；

(2)、直接写出关于x的不等式kx+b＞ $\frac{m}{x}$ 的解集．

查看试题解析
22. 如图，在平面直角坐标系中，O为坐标原点，抛物线y＝x²+2x与x轴的另一个交点为A，把该抛物线在x轴及其下方的部分记作C₁ ，将C₁绕着点O旋转180°，得到C₂ ， C₂与x轴交于另一点B．

(1)、求抛物线C₂的顶点E的坐标；

(2)、将C₂绕着点B旋转180°得到C₃ ，连接C₁与C₃的最低点，则阴影部分图形的面积为．

查看试题解析
23. 如图，AB是⊙O的直径，AB＝6，AC切⊙O于点A，BC交⊙O于点D，∠C＝50°．

(1)、求∠B的度数；

(2)、求 $\overset{⌢}{A D}$ 的长．

查看试题解析
24. 为了预防“流感”，某学校对教室采用药熏法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与药物点燃后的时间x（分）满足函数关系式y＝2x，药物点燃后6分钟燃尽，药物燃尽后，校医每隔6分钟测一次空气中含药量，测得数据如下表：
药物点燃后的时间x（分）
6
12
18
24
空气中的含药量y（毫克/立方米）
12
6
4
3

(1)、在如图所示平面直角坐标系中描出以表格中数据为坐标的各点；

(2)、观察上述各点的分布规律，判断它们是否在同一个反比例函数图象上，如果在同一个反比例函数图象上，求出这个反比例函数图象所对应的函数表达式，如果不在同一个反比例函数图象上，说明理由；

(3)、研究表明：空气中每立方米的含药量不低于8毫克，且持续4分钟以上才能有效杀灭空气中的病菌，应用上述发现的规律估算此次消毒能否有效杀灭空气中的病菌？

查看试题解析
25. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点 $D$ 、 $E$ 在 $B C$ 边上， $∠ D A E = 45 °$ ，将 $△ A C E$ 绕点 $A$ 顺时针旋转 $90 °$ 得 $△ A B F$ ．

(1)、求证： $B F ⊥ B C$ ；

(2)、连接 $D F$ ，求证： $△ A D F ≌ △ A D E$ ；

(3)、若 $B D = 3$ ， $C E = 4$ ，则 $D F =$ ，四边形 $A F D E$ 的面积＝．

查看试题解析
26. 如图，抛物线y＝x²+bx+c（b、c是常数）与x轴交于点A(﹣1，0)和点B(3，0)，与y轴交于点C．P为抛物线上一点，横坐标为m．

(1)、求此抛物线的解析式；

(2)、△ABP面积记为S，当0≤m≤ $\frac{5}{2}$ 时，求S的取值范围．

(3)、当此抛物线在点C与点P之间部分（含点C和点P）最高点与最低点的纵坐标之差为2时，求m的值．

查看试题解析

摸球的次数n	500	1000	2000	2500	3000	5000
摸到红球的次数m	351	722	1486	1870	2262	3760
摸到红球的频率 $\frac{m}{n}$	0.702	0.722	0.743	0.748	0.754	0.752

药物点燃后的时间x（分）	6	12	18	24
空气中的含药量y（毫克/立方米）	12	6	4	3

x	…	﹣1	1	2	3	4	…
y	…	﹣6	﹣2	﹣3	﹣6	﹣11	…