吉林省吉林市舒兰市2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-10-11 类型：期末考试
一、单选题
-
1. 一元二次方程x2+x﹣2=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根2. 将抛物线y＝﹣3x2平移，得到抛物线y＝﹣3（x+1）2+2，下列平移方式中，正确的是（ ）A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向上平移2个单位 D、先向右平移1个单位，再向下平移2个单位3. 已知反比例函数 ，下列结论中错误的是（ ）A、图象经过点(-1,-1) B、图象在第一、三象限 C、当 时， D、当 时，y随着x的增大而增大4. 国旗上的五角星是旋转对称图形，它需要旋转（ ）后，才能与自身重合．A、36° B、45° C、60° D、72°5. 一个不透明的盒子里有n个除颜色外其他完全相同的小球，其中有9个黄球，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么估计盒子中小球的个数n为（ ）A、20 B、24 C、28 D、306. 如图，AB是⊙O的直径，C、D是⊙O上一点，∠CDB=25°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于（ ）
A、40° B、50° C、60° D、70°二、填空题
-
7. 已知k＞0，且关于x的方程3kx2+12x+k+1=0有两个相等的实数根，那么k的值等于 ．8. 如图，直线AlA∥BB1∥CC1 ， 若AB=8，BC=4，A1B1=6，则线段A1C1的长是 ．
9. 如图，双曲线 经过点A(2，2)与点B(4， )，则△AOB的面积为.
10. 如图，在边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AE的长为 ．
11. 如图，△ABC三个顶点的坐标分别为A（2，2），B（4，2），C（6，4），以原点O为位似中心，将△ABC缩小为原来的一半，则线段AC的中点P变换后在第一象限对应点的坐标为 ．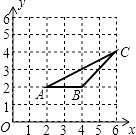
12. 如图，在△ABC中，点D在AB上，点E在AC上，∠ADE=∠C，四边形DBCE的面积是△ADE面积的3倍．若DE=3，则BC的长为 ．
13. 如图，AB是⊙O的直径， BC切⊙O于点B ， AC交⊙O于点D ． 若⊙O的半径为3，∠C＝40°，则 的长为 ． （结果保留π）
14. 如图，杂技团进行杂技表演，一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线 的一部分，跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高．若人梯到起跳点A的水平距离为4米，则人梯BC的高为米．
三、解答题
-
15. 解方程：x(x-1)=2．16. 已知：在平面直角坐标系中，△ABC 的三个顶点的坐标分别为 A(5，4)、B(0，3)、(2，1)
⑴画出△ABC 关于原点成中心对称的△；
⑵画出将△ 绕点 按顺时针旋转90°所得的 ， 并写出点的坐标
17. 甲、乙两名同学玩一个游戏：在一个不透明的口袋中装有三个小球，分别标有数字1、2、3，这些小球除数字不同外其余均相同．甲先从口袋中随机摸出一个小球记下数字后放回，搅匀后乙再从口袋中随机摸出一个小球．若两次摸出的小球上数字之和是偶数则甲获胜；若两次摸出的小球上数字之和是奇数，则乙获胜．用画树状图或列表的方法，说明这个游戏对双方是否公平．18. 如图，在△ABC中，∠ABC＝90°，AB＝BC＝2，以点C为圆心，线段CA的长为半径作弧AD，交CB的延长线于点D，求出阴影部分的面积（结果保留π）．
19. 如图，△ABC 中，∠B＝10°，∠ACB＝20°，AB＝4cm，三角形 ABC 按逆时针方向旋转一定角度后与三角形 ADE 重合，且点 C 恰好成为 AD 的中点.
(1)、指出旋转中心，并求出旋转的度数；(2)、求出∠BAE 的度数和 AE 的长.20. 如图，在平面直角坐标系中，点A的坐标为（0，2），点B的坐标为（4，2）．若抛物线（h、k为常数）与线段AB交于C、D两点，A、B也关于抛物线对称轴对称，且CD＝AB，求抛物线的解析式．
21. 如图，一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象在第一象限内交于A(1，6)，B(3，n)两点．请解答下列问题：
(1)、求这两个函数的表达式；(2)、根据图象直接写出kx+b﹣>0的x的取值范围．22. 如图，有一直径为4的圆形铁皮，要从中剪出一个最大圆心角为60°的扇形ABC．
(1)、求剪下的扇形ABC（即阴影部分）的半径；(2)、若用此剪下的扇形铁皮围成一个圆锥形铁帽，求此圆锥形铁帽的底面圆的半径r．23. 某书店销售一批教辅书籍，每天可售出20套，每套可盈利40元，为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一套书每降价1元，每天可多售出2套．请解答下列问题：(1)、设每套降价x元，每天盈利y元（不计其他书籍），求y与x之间的函数关系式(2)、若书店每天想要在此教辅书上盈利1200元，每套应降价多少元？(3)、每套降价多少元时，书店每天销售这套教辅书的盈利达到最大？盈利最大是多少元？24. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E．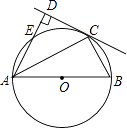
(1)、求证：AC平分∠DAB；(2)、若∠B=60°，CD=2 ，求AE的长．25. 如图：
(1)、【问题探究】如图1，△ABC和△DEC均为等腰直角三角形，∠ACB=∠DCE=90°，点B，D，E在同一直线上，连接AD，BD．
①请写出AD与BD之间的位置关系： ▲ ；
②若AC=BC= ， DC=CE= ， 求线段AD的长；
(2)、【拓展延伸】如图2，△ABC和△DEC均为直角三角形，∠ACB=∠DCE=90°，AC= ， BC= ， CD= ， CE=1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD，连接AD，当点B，D，E在同一直线上时，直接写出线段AD的长．
26. 如图，在平面直角坐标系中，矩形ABCD的边AB在轴上，AB、BC的长分别是一元二次方程x2-7x+12=0的两个根，其中BC＞AB，OA=2OB，边CD交y轴于点E，动点P以每秒1个单位长度的速度，从点E出发沿折线段ED—DA向点A运动，运动的时间为t（0＜t＜6）秒，设△BOP与矩形AOED重叠部分的面积为s．请解答下列问题：
(1)、求点D的坐标；(2)、求s关于t的函数关系式，并写出自变量的取值范围；(3)、在点P的运动过程中，是否存在点P，使△BEP为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．