黑龙江省齐齐哈尔市依安县2021-2022学年九年级上学期期末数学试题2
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、3. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球4. 如图,在△ABC中,AC=BC=8,∠BCA=60°,直线AD⊥BC于点D,E是AD上的一个动点,连接EC,将线段EC绕点C按逆时针方向旋转60°得到FC,连接DF,则在点E的运动过程中,DF的最小值是( )
2. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、3. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球4. 如图,在△ABC中,AC=BC=8,∠BCA=60°,直线AD⊥BC于点D,E是AD上的一个动点,连接EC,将线段EC绕点C按逆时针方向旋转60°得到FC,连接DF,则在点E的运动过程中,DF的最小值是( )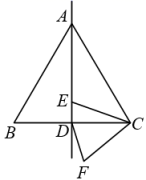 A、1 B、1.5 C、2 D、45. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
A、1 B、1.5 C、2 D、45. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( ) A、116° B、32° C、58° D、64°6. 将抛物线y=4x2向右平移1个单位,再向上平移3个单位,得到的抛物线是( )A、y=4(x+1)2+3 B、y=4(x﹣1)2+3 C、y=4(x+1)2﹣3 D、y=4(x﹣1)2﹣37. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )A、
A、116° B、32° C、58° D、64°6. 将抛物线y=4x2向右平移1个单位,再向上平移3个单位,得到的抛物线是( )A、y=4(x+1)2+3 B、y=4(x﹣1)2+3 C、y=4(x+1)2﹣3 D、y=4(x﹣1)2﹣37. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )A、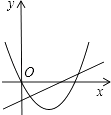 B、
B、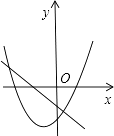 C、
C、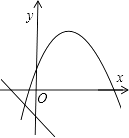 D、
D、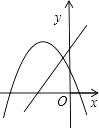 8. 抛物线y=x2-2x-4的顶点M关于坐标原点O的对称点为N,则点N的坐标为( )A、(1,-5) B、(1,5) C、(-1,5) D、(-1,-5)9. 如图所示,A,B,C,D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P,Q两点从出发开始几秒时,点P和点Q的距离是10cm.(若一点到达终点,另一点也随之停止运动)( )
8. 抛物线y=x2-2x-4的顶点M关于坐标原点O的对称点为N,则点N的坐标为( )A、(1,-5) B、(1,5) C、(-1,5) D、(-1,-5)9. 如图所示,A,B,C,D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P,Q两点从出发开始几秒时,点P和点Q的距离是10cm.(若一点到达终点,另一点也随之停止运动)( ) A、2s或s B、1s或s C、s D、2s或s10. 如图抛物线 的对称轴为直线 ,与x轴一个交点在 和 之间,其部分图象如图所示.则下列结论:① ;② ;③ ;④ (t为实数);⑤点 , , 是该抛物线上的点,则 .正确的个数有( )
A、2s或s B、1s或s C、s D、2s或s10. 如图抛物线 的对称轴为直线 ,与x轴一个交点在 和 之间,其部分图象如图所示.则下列结论:① ;② ;③ ;④ (t为实数);⑤点 , , 是该抛物线上的点,则 .正确的个数有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 当 时,二次函数 有最小值.12. 若关于x的一元二次方程 的一个根是0,则a的值是13. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转某个角度后得到△A′B′C,当点A的对应点A′落在AB边上时,阴影部分的面积为.
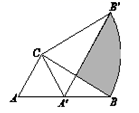 14. 若关于的一元二次方程有两个不相等实数根,则k的取值范围是 .15. 将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是度16. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .17. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“”的路线运动,设第n秒运动到点(n为正整数),则点的坐标是 .
14. 若关于的一元二次方程有两个不相等实数根,则k的取值范围是 .15. 将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是度16. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .17. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“”的路线运动,设第n秒运动到点(n为正整数),则点的坐标是 .
三、解答题
-
18. 解方程: .19. 已知关于x的一元二次方程两个不相等的实数根 , , 若 , 求m的值.20. 如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OEBD,连接BE,DE,BD,若BE交AC于点F,若∠DEB=∠DBC.
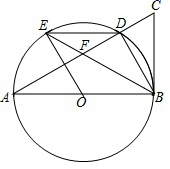 (1)、求证:BC是⊙O的切线;(2)、若BF=BC=2,求AB的长.21. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)、求证:BC是⊙O的切线;(2)、若BF=BC=2,求AB的长.21. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)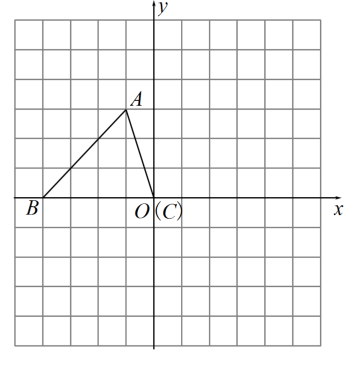
⑴画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
⑵画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
⑶在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
22. 某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.(1)、求每次下降的百分率.(2)、若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?(3)、在(2)的条件下,若使商场每天的盈利达到最大值,则应涨价多少元?此时每天的最大盈利是多少?23. 如图,已知抛物线与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,其顶点为D. (1)、求抛物线及直线AC的函数关系式,并直接写出点D的坐标;(2)、若P是抛物线上位于直线AC上方的一个动点,当点P的坐标为多少时,△APC的面积有最大值.(3)、点Q在平面内,试探究是否存在以A,C,D,Q为顶点的平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线及直线AC的函数关系式,并直接写出点D的坐标;(2)、若P是抛物线上位于直线AC上方的一个动点,当点P的坐标为多少时,△APC的面积有最大值.(3)、点Q在平面内,试探究是否存在以A,C,D,Q为顶点的平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.