黑龙江省齐齐哈尔市龙江县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 已知关于 $x$ 的方程 $x^{2} - k x - 6 = 0$ 的一个根为 $x = 3$ ，则实数 $k$ 的值为 $($ $)$

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
2. “学习强国”APP是一款提供优质学习资源的客户端应用，下面是应用内的几个子频道图标，其中图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把抛物线y＝x²向右平移1个单位长度，再向上平移3个单位长度，得到的抛物线解析式是（　　）

A、y＝（x+1）²+3 B、y＝（x+1）²﹣3 C、y＝（x﹣1）²﹣3 D、y＝（x﹣1）²+3

查看试题解析
4. 如图，已知⊙O的直径 $C D = 8$ ， $A B$ 是⊙O的弦， $A B ⊥ C D$ ，垂足为 $M$ ， $O M = 2$ ，则 $A B$ 的长为（）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{3}$

查看试题解析
5. 下列事件中是必然事件的是（）

A、小明买一张体育彩票中奖 B、某人的体温是100 ℃ C、抛掷一枚骰子朝上的面的点数是偶数 D、我们小组的十三位同学中至少有两位同学是同月出生的

查看试题解析
6. 关于x的一元二次方程﹣kx²﹣6x+3＝0有两个不相等的实数根，则k的取值范围是（）

A、k＞﹣3 B、k＜3 C、k＜3且k≠0 D、k＞﹣3且k≠0

查看试题解析
7. 2019年12月以来，湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病．感染者的临床表现为：以发热、乏力、干咳为主要表现．在“新冠”初期，有1人感染了“新冠”，经过两轮传染后共有144人感染了“新冠”（这两轮感染因为人们不了解病毒而均未被发现未被隔离），则每轮传染中平均一个人传染了（）

A、10人 B、11人 C、12人 D、13人

查看试题解析
8. 如图，四边形ADBC内接于⊙O，∠AOB＝122°，则∠ACB等于（　　）

A、131° B、119° C、122° D、58°

查看试题解析
9. 如图，将含有 $60 °$ 锐角的三角板 $Δ A B C$ 绕 $60 °$ 的锐角顶点 $C$ 逆时针旋转一个角度到 $Δ E C D$ ，若 $A B$ 、 $C E$ 相交于点 $F$ ， $A E = A F$ ，则旋转角是（）

A、 $45 °$ B、 $40 °$ C、 $35 °$ D、 $30 °$

查看试题解析
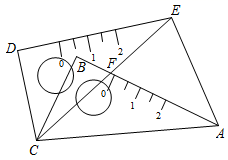10. 对称轴为直线x＝1的抛物线y＝ax²＋bx＋c（a、b、c为常数，且a≠0）如图所示，现有结论：①abc＜0，②b²＞4ac，③3a＋c＞0，④ac﹣bc＋c²＜0，其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 点 $A (4 ， n)$ 和点 $B (m ， 3)$ 关于原点对称，则 $m + n =$ ．

查看试题解析
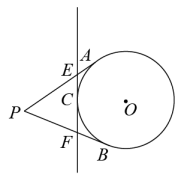
12. 若方程ax²+2x-1=2x²是关于x的一元二次方程，则a的取值范围是．

查看试题解析
13. 将圆心角为 $120 °$ 的扇形围成底面圆的半径为 $1 c m$ 的圆锥，则圆锥的母线长为．

查看试题解析
14. 如图，PA、PB分别与⊙O相切于点A、B，直线EF与⊙O相切于点C，分别交PA、PB于E、F，且PA＝8cm，则△PEF的周长为 cm．

查看试题解析
15. 如图，在 $⊙ O$ 中， $O A = 3$ ， $∠ C = 45 °$ ，则图中阴影部分的面积是.（结果保留 $π$ ）

查看试题解析
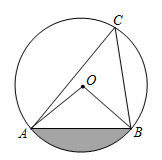16. 如图，已知正方形 $A B C D$ ，将边 $C D$ 绕点 $C$ 顺时针旋转45°，得到线段 $C E$ ，连接 $D E$ 、 $A E$ ， $D C = 2$ ，则 $A E$ 的长为．

查看试题解析
17. 如图，在平面直角坐标系中，边长为1个单位长度的正六边形ABCDEF的对角线AD在x轴上，AO＝DO，将该正六边形绕原点O逆时针旋转，第1次与原正六边形重合时，点A落在原正六边形的顶点B处，第2次与原正六边形重合时，点A落在原正六边形的顶点C处，第3次与原正六边形重合时，点A落在原正六边形的顶点D处，…，第2021次重合时点A的坐标为．

查看试题解析

三、解答题

18. 计算：（π﹣3）⁰+（﹣ $\frac{1}{3}$ ）^﹣²﹣|1﹣ $\sqrt{2}$ |+ $\sqrt{18}$ ．

查看试题解析
19. 用适当方法解下列方程：

(1)、3x²﹣2x﹣1＝0；

(2)、x（x+2）＝2x+4．

查看试题解析
20. 2021年是“十四五”规划开局之年，也是中国共产党建党100周年，为加强党史学习教育，学校决定在周二、周三、周四的活动课分别组织三场“从小学党史，永远跟党走”的演讲活动．小红和小明打算随机选择时间去观摩演讲，已知，小红和小明选择上述三天中哪一天去观摩演讲的可能性是相同的．

(1)、小红选中周四去观摩演讲的概率是．

(2)、请你用列表法或画树状图法，求小红和小明选择同一天去观摩演讲的概率．

查看试题解析
21. 如图，以等边三角形ABC的BC边为直径画圆，交AC于点D ， $D F ⊥ A B$ 于点F ，连接OF ，且 $A F = 1$ ．

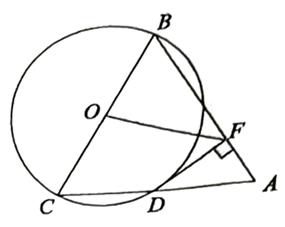(1)、求证：DF是 $⊙ O$ 的切线；

(2)、求线段OF的长度．

查看试题解析
22. 某公司经过市场调查，整理出某种商品在某个月的第 $x$ 天与日销售量的相关信息如下表：
第 $x$ 天
售价/（元/件）
日销售量/件
$1 ⩽ x ⩽ 30$
$x + 40$
$100 - 2 x$
已知商品的进价为20元/件，设该商品的日销售利润为 $y$ 元．

(1)、 $y$ 与 $x$ 的函数关系式为；

(2)、在销售该商品的第几天时，日销售利润为2250元？

(3)、当售价为多少元时，日销售利润最大？最大利润为多少？

查看试题解析
23. 综合与实践
动手操作：利用“正方形纸片的折叠和旋转”开展数学活动，探究体会图形在正方形折叠和旋转过程中的变化及其蕴含的数学思想方法．
折一折：如图1，已知正方形ABCD的边长AB＝6，将正方形ABCD沿过点A的直线折叠，使点B的对应点M落在AC上，展开正方形ABCD，折痕为AE，延长EM交CD于点F，连接AF．

(1)、思考探究：图1中，与△ABE全等的三角形有个，∠EAF＝°，BE、EF、DF三者的数量关系是， BE的长为．

(2)、转一转：将图1中的∠EAF绕点A旋转到图2所示位置，与BC、CD的交点分别为E、F，连接EF．
证明推理：图2中，BE、EF、DF三者的数量关系是 ▲ ，并给出证明．

(3)、开放拓展：如图3，在旋转∠EAF的过程中，当点F为CD的中点时，BE的长为．

查看试题解析
24. 已知抛物线y＝ax²+bx+3的图象与x轴相交于点A和点B（1，0），与y轴交于点C，连接AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F，AB＝4，设点D的横坐标为m．

(1)、求抛物线的解析式；

(2)、当m＝﹣1时，在x轴上找一点P，使PE+PC的值最小，求出此时点P的坐标；

(3)、连接AE、CE，当△ACE的面积最大时，点D的坐标是；

(4)、当m＝﹣2时，在平面内是否存在点Q，使以B，C，E，Q为顶点的四边形为平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

第 $x$ 天	售价/（元/件）	日销售量/件
$1 ⩽ x ⩽ 30$	$x + 40$	$100 - 2 x$