黑龙江省七台河市勃利县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程是一元二次方程的是（）

A、 $3 x^{4} + 2 x^{5} = 0$ B、 $(2 y^{2} + 4)^{2} - 9 = 0$ C、 $\frac{1}{5} x^{2} + 3 x + \frac{1}{2} = 0$ D、 $\frac{1}{x + 2} \cdot \frac{1}{x - 2} = 4$

查看试题解析
3. 抛物线 $y = x^{2} + 4$ 与y轴的交点坐标是（　　）

A、（4，0） B、（-4，0） C、（0，-4） D、（0，4）

查看试题解析
4. 如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（　　）

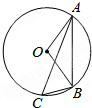A、30° B、40° C、45° D、50°

查看试题解析
5. 同时掷两枚骰子，点数和为4的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{11}$ D、 $\frac{1}{24}$

查看试题解析
6. 方程x²﹣9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（）

A、12 B、15 C、12或15 D、不能确定

查看试题解析
7. 若一次函数y=ax+b（a≠0）的图象与x轴的交点坐标为（﹣2，0），则抛物线y=ax²+bx的对称轴为（）

A、直线x=1 B、直线x=﹣2 C、直线x=﹣1 D、直线x=﹣4

查看试题解析
8. 若一个圆锥的母线长是它底面半径的3倍，则它的侧面展开图的圆心角等于（）

A、120° B、135° C、150° D、180°

查看试题解析
9. 某化肥厂生产的化肥经过两年增长了21%，则每年比上一年平均增长的百分数是（）

A、12% B、10% C、9% D、7.9%

查看试题解析
10. 函数y=x²+bx+c与y=x的图象如图所示，有以下结论：①b²﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x²+（b﹣1）x+c＜0．
其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知点 $M (a ， b - 2)$ 与点 $N (b ， 4 - a)$ 关于原点对称，则 $a b =$ ．

查看试题解析
12. 已知 $(x^{2} + y^{2} + 1) (x^{2} + y^{2} - 3) = 5$ ，则 $x^{2} + y^{2}$ 的值等于.

查看试题解析
13. 若两个圆的半径分别为3和4，圆心之间的距离是5，则这两个圆的位置关系是．

查看试题解析
14. 点 $A (2 ， y_{1})$ 、 $B (3 ， y_{2})$ 是二次函数 $y = x^{2} - 2 x + 1$ 的图象上两点，则 $y_{1}$ 与 $y_{2}$ 的大小关系为 $y_{1}$ $y_{2}$ （填“＞”、“＜”、“＝”）.

查看试题解析
15. 若关于x的一元二次方程 $n x^{2} - 2 x - 1 = 0$ 无实数根，则一次函数 $y = (n + 1) x - n$ 的图象不经过第象限．

查看试题解析
16. 在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是 $\frac{2}{5}$ ，如再往盒中放进3颗黑色棋子，取得白色棋子的概率变为 $\frac{1}{4}$ ，则原来盒里有白色棋子颗．

查看试题解析
17. 如图， $A B$ 是半圆 $O$ 的直径，弦 $A C$ 与 $A B$ 成30°的角， $A C = C D$ ，若 $O A = 2$ ，则 $A C$ 的长是．

查看试题解析
18. 如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，则图中阴影部分面积为．

查看试题解析
19. 如图，△ABC中，AB=AC，∠A为锐角，CD为AB边上的高，点O为△ACD的内切圆圆心，则∠AOB= ．

查看试题解析
20. 如图，在平面直角坐标系中，点A、B的坐标分别为（﹣5，0）、（﹣2，0）．点P在抛物线y=﹣2x²+4x+8上，设点P的横坐标为m．当0≤m≤3时，△PAB的面积S的取值范围是．

查看试题解析

三、解答题

21. 解方程

(1)、 $x^{2} - 2 \sqrt{2} x + 1 = 0$ ；

(2)、 $x^{2} - 4 x - 21 = 0$ ．

查看试题解析
22. 如图， $△ A B C$ 中 $A (- 2 ， 3)$ ， $o$ ， $C (- 1 ， 2)$ ．
⑴将 $△ A B C$ 向右平移4个单位长度，画出平移后的 $△ A_{1} B_{1} C_{1}$ ；
⑵画出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{2} B_{2} C_{2}$ ；
⑶将 $△ A B C$ 绕原点 $O$ 旋转 $18 0^{∘}$ ，画出旋转后的 $△ A_{3} B_{3} C_{3}$ ；
⑷在 $△ A_{1} B_{1} C_{1}$ ， $△ A_{2} B_{2} C_{2}$ ， $△ A_{3} B_{3} C_{3}$ 中，哪些是成轴对称的，对称轴是什么？
哪些是成中心对称的，对称中心的坐标是什么？

查看试题解析
23. 已知关于x的一元二次方程x²﹣4x+m﹣1=0有两个相等的实数根，求m的值及方程的根．

查看试题解析
24. 如图，已知在平面直角坐标系中， $O$ 为坐标原点，二次函数 $y = x^{2} + b x + c$ 的图象与 $x$ 轴的负半轴相交于点 $A$ ，与 $x$ 轴的正半轴相交于点 $B$ ，与 $y$ 轴相交于点 $C$ ，点 $C$ 的坐标为（0，-3），且 $B O = C O$ ．

(1)、求这个二次函数的解析式；

(2)、设这个二次函数的顶点为 $M$ ，求 $A M$ 的长．

查看试题解析
25. 把一副普通扑克牌中的4张；黑桃2，红心3，梅花4，黑桃5，洗匀后正面朝下放在桌面上.

(1)、从中随机抽取一张牌是黑桃的概率是多少？

(2)、从中随机抽取一张，再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果，并求抽取的两张牌牌面数字之和大于7的概率.

查看试题解析
26. 如图， $A C$ 为⊙O的直径，过点 $C$ 的切线与弦 $A B$ 的延长线交于点 $D$ ， $O E$ 为半径， $O E ⊥ A B$ 于点 $H$ ，连接 $C E ， C B$ ．

(1)、求证： $∠ C O E = 2 ∠ D C E$ ；

(2)、若 $A B = 8 ， E H = 2$ ，求 $C E$ 的长．

查看试题解析
27. 九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：

时间x（天）

1≤x＜50

50≤x≤90

售价（元/件）

x＋40

90

每天销量（件）

200－2x

已知该商品的进价为每件30元，设销售该商品的每天利润为y元[

(1)、求出y与x的函数关系式；

(2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？

(3)、该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.

查看试题解析
28. 如图，在平面直角坐标系中，点 $O$ 为坐标原点，直线 $y = - x + 3$ 与 $x$ 轴， $y$ 轴分别交于 $B ， C$ 两点，抛物线 $y = a x^{2} + b x + 3$ 经过点 $B$ ，对称轴为直线 $x = 1$ ．

(1)、求 $a ， b$ 值；

(2)、 $P$ 是直线 $B C$ 上方抛物线上任意一点，设点 $P$ 的横坐标为 $t$ ， $Δ P B C$ 的面积为 $S$ ，求 $S$ 与 $t$ 之间的函数关系式，并写出 $t$ 的取值范围．

查看试题解析

时间x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x＋40	90
每天销量（件）	200－2x