黑龙江省宁安市2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列交通标志图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）．

A、 $2 a^{2} \cdot 3 b^{2} = 6 a^{5} b^{5}$ B、 $(- 2 a)^{2} = - 4 a^{2}$ C、 $(a^{5})^{2} = a^{7}$ D、 $x^{- 2} = \frac{1}{x^{2}} (x \neq 0)$

查看试题解析
3. 将分别标有“文”“明”“宁“安”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀，随机摸出一球，不放回；再随机摸出一球，两次摸出的球上的汉字组成“宁安”的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 某几何体的主视图如图所示，它的左视图不可能的是（）
主视图

A、 B、 C、 D、

查看试题解析
5. 已知抛物线y=mx²+nx和直线y=mx+n在同一坐标系内的图像如图，其中正确的是（）

A、 B、 C、 D、

查看试题解析
6. 在 $△ A B C$ 中， $A B = 12 \sqrt{2} ， A C = 13 ， c o s B = \frac{\sqrt{2}}{2}$ ，则 $B C$ 边长为（）

A、7 B、8 C、7或17 D、8或17

查看试题解析
7. 若关于x的分式方程 $\frac{2 x - a}{x - 2} = \frac{1}{2}$ 的解为非负数，则a的取值范围是（　　）

A、a≥1 B、a＞1 C、a≥1且a≠4 D、a＞1且a≠4

查看试题解析
8. 如图，AB为⊙O的直径，AB＝6，AB⊥弦CD，垂足为G，EF切⊙O于点B，∠A＝30°，连接AD，OC，BC，下列结论错误的是（）

A、EF∥CD B、△COB是等边三角形 C、CG＝DG D、 $\overset{⌢}{B C}$ 的长为 $\frac{3 π}{2}$

查看试题解析
9. 如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处．已知AB＝8，sin∠EFC= $\frac{3}{5}$ ，则BC的值为（）

A、8 B、9 C、10 D、12

查看试题解析
10. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ，将 $Δ A B C$ 绕点 $C$ 顺时针旋转得到 $Δ E D C$ ，点 $M$ 是 $B C$ 中点，点 $N$ 是 $D E$ 中点，连接 $M N$ ，若 $∠ A = 30 ° ， A C = 4 \sqrt{3}$ ，则线段 $M N$ 的最大值是（）

A、 $2 \sqrt{7}$ B、6 C、4 D、3

查看试题解析
11. 如图，延长等腰 $R t Δ A B C$ 斜边 $A B$ 到 $D$ ，使 $B D = 2 A B$ ，连接 $C D$ ，则 $t a n ∠ B C D$ 的值为（）

A、 $\frac{2}{3}$ B、1 C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 如图，在矩形 $A B C D$ 中，对角线 $A C 、 B D$ 相交于点 $O$ ， $E$ 为 $C D$ 的中点，连接 $A E$ 交 $B D$ 于点 $F$ ，连接 $C F$ ， $∠ A F D = 90 °$ ，则下列结论：① $∠ A E D = ∠ O B C$ ；② $A F = C F$ ③ $S_{Δ A D F} = S_{Δ A F C}$ ；④ $C D^{2} = 4 A E \cdot E F$ ，其中正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 黑龙江省土地面积约为45.4万平方千米，这个数用科学记数法表示为平方千米．

查看试题解析
14. 在函数 $y = \frac{x^{2}}{\sqrt{x + 2}}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
15. 某商品进价为180元，标价为270元，打八折售出，则这件商品获得的利润为．

查看试题解析
16. 如图，要使 $Δ A B C$ 与 $Δ A D E$ 相似，则需添加一个适当的条件是(只添一个即可)．

查看试题解析
17. 一个圆锥的底面周长是6 $π$ cm，母线长是6cm，则圆锥侧面积展开图的扇形圆心角是．

查看试题解析
18. 若 $m ， n$ 是 $x^{2} - x - 2020 = 0$ 的两个实数根，则 $m^{2} + m + 2 n$ 的值为．

查看试题解析
19. 按顺序观察下列五个数-1，5，-7，17，-31……，找出以上数据依次出现的规律，则第 $n$ 个数是．

查看试题解析
20. 如图，正方形ABCD的边长为3，AD边在x轴负半轴上，反比例函数y= $\frac{k}{x}$ （x＜0）的图象经过点B和CD边中点E，则k的值为．

查看试题解析
21. 菱形 $O A B C$ 如图放置，点 $C$ 坐标是(3，4)，先将菱形向左平移6个单位长度，向上平移1个单位长度，然后沿 $x$ 轴翻折，最后绕坐标原点 $O$ 旋转90°得到菱形 $O A B C$ 的对角线交点的对应点为点 $P$ ，则点 $P$ 的坐标是．

查看试题解析
22. 如图，已知顶点为（-3，-6）的抛物线 $y = a x^{2} + b x + c$ 经过点（-1，-4），则下列结论：① $b^{2} > 4 a c$ ② $a x^{2} + b x + c ≥ - 6$ ③若点 $(- 2 ， m) ， (- 5 ， n)$ 在抛物线上，则 $m > n$ ④关于 $x$ 的一元二次方程 $a x^{2} + b x + c = - 4$ 的两根为-5和-1 ⑤ $(a + c)^{2} > b^{2}$ ，其中正确的有．

查看试题解析

三、解答题

23. 先化简，再求值： $(\frac{1}{x} - \frac{2}{x + 1}) \div \frac{2 x - 2 x^{2}}{x^{2} + 2 x + 1} ，$ 其中x满足 $x^{2} - x - 1 = 0$

查看试题解析
24. 如图，抛物线的顶点为C（1，4），交x轴于点A，B ( -1，0 ) 两点，交y轴于点D．

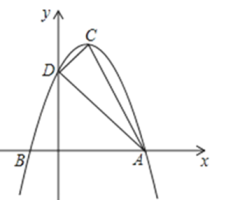(1)、求抛物线的解析式，并直接写出点D的坐标，

(2)、判断△ACD的形状，并求出△ACD的面积．

查看试题解析
25. 平行四边形 $A B C D$ 的对角线 $A C ， B D$ 相交于点 $O$ ， $O B = 5 ， A B = 8 ， B C = 6 ，$ 以 $O A$ 为边作正方形 $O A E F$ ，过点作 $E P ⊥ A B$ 交直线 $A B$ 于点 $P$ ，连接 $P C$ ．请画出正确的图形，并直接写出 $C P$ 的长．

查看试题解析
26. 正方形 $A B C D$ ，点 $E$ 在直线 $A C$ 上，点F在直线BC上， $E F ⊥ D E ， E N ⊥ D C$ ，垂足是 $N$ ．

(1)、当点 $F$ 在边 $B C$ 上时，如图①，求证： $D N + C F = E N$ ；

(2)、当点 $F$ 在 $B C$ 的延长线上时，如图②；当点 $F$ 在 $C B$ 的延长线上时，如图③，直接写出线段 $D N ， C F ， E N$ 之间的数量关系，不需要证明；

(3)、在（1）、（2）的的条件下若 $C N = 2 \sqrt{2} A E = 8$ ，则 $C F$ = ．

查看试题解析
27. 我市某文具店准备购进A、B两种文具，A种文具每件的进价比B种文具每件的进价多20元，用5000元购进A种文具的数量和用3000元购进B种文具的数量相同．文具店将A种文具每件的售价定为80元，B种文具每件的售价定为45元

(1)、A种文具每件的进价和B种文具每件的进价各是多少元?

(2)、文具店计划用不超过1600元的资金购进A、B两种文具共40件，其中A种文具的数量不低18件，该文具店有几种进货方案？

(3)、在(2)的条件下，文具店利用销售这40件文具获得的最大利润再次购进A、B两种文具，且再次销售过程中B种文具每件的售价提高了5元，直接写出再次购进A、B两种文具获利最大的进货方案．

查看试题解析
28. 如图，在平面直角坐标系中，直线 $A B$ 与 $x$ 轴、 $y$ 轴分别交于点A、B，直线 $C D$ 与 $x$ 轴、 $y$ 轴分别交于点 $C 、 D$ ， $A B$ 与 $C D$ 相交于点 $E$ ，线段 $O A 、 O C$ 的长是一元二次方程 $x^{2} - 18 x + 72 = 0$ 的两根(OA＞OC)， $B E = 5$ ， $t a n ∠ A B O = \frac{3}{4}$ ．

(1)、求点 $A 、 C$ 的坐标

(2)、若反比例函数 $y = \frac{k}{x}$ 的图象经过点E，求 $k$ 的值

(3)、若点 $P$ 在坐标轴上，在平面内是否存在一点 $Q$ ，使以点C、E、P、Q为顶点的四边形是矩形？若存在，请写出满足条件的点 $Q$ 的个数，并直接写出其中两个点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析