黑龙江省牡丹江市林口县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. “垃圾分一分，环境美十分”下列四种垃圾回收标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下说法正确的是（）

A、在367人中至少有两个人的生日相同 B、一次摸奖活动的中奖率是1%，那么摸100次必然会中一次奖 C、一副扑克牌中，随意抽取一张是红桃K，这是必然事件 D、一个不透明的袋中装有3个红球，5个白球，搅匀从中任意摸出一个球，摸到红球的可能性大于摸到白球的可能性

查看试题解析
3. 下列说法其中正确的是（）

A、有一个角等于30°的两个等腰三角形相似； B、有一个角等于120°的两个等腰三角形相似； C、相似三角形一定不是全等三角形； D、相似三角形对应角平分线的长度比等于面积比．

查看试题解析
4. 反比例函数y＝ $（ a - 1) x^{a}$ 的图象在（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
5. $y = m x^{m^{2} + 1}$ 是二次函数，则m的值是（）

A、m≠0 B、m＝±1 C、m＝1 D、m＝﹣1

查看试题解析
6. 如图，⊙O的直径AB垂直于弦CD，垂足为E．如果∠B＝60°，AC＝6，那么CD的长为（）

A、8 B、6 $\sqrt{3}$ C、6 $\sqrt{2}$ D、6

查看试题解析
7. 如图，将△ABC绕点A逆时针旋转至△ADE，使点C落在DE上，若∠EAB＝90°，∠BCD＝40°，则∠CAD的度数为（）

A、10° B、20° C、30° D、40°

查看试题解析
8. 若关于x的一元二次方程（k-1）x²﹣2kx+ k-3=0有实数根，则k的取值范围为（）

A、k> $\frac{3}{4}$ B、k> $\frac{3}{4}$ 且k≠1 C、k≥ $\frac{3}{4}$ D、k≥ $\frac{3}{4}$ 且k≠1

查看试题解析
9. 如图，在矩形 $A B C D$ 中， $A D = 8$ ， $E$ 是边 $A B$ 上一点，且 $A E = \frac{1}{4} A B$ ．已知 $⊙ O$ 经过点 $E$ ，与边 $C D$ 所在直线相切于点 $G$ （ $∠ G E B$ 为锐角），与边 $A B$ 所在直线交于另一点 $F$ ，且 $E G ： E F = \sqrt{5} ： 2$ ，当边 $A D$ 或 $B C$ 所在的直线与 $⊙ O$ 相切时， $A B$ 的长是（）

A、9 B、4 C、12或4 D、12或9

查看试题解析
10. 如图，正方形被分割成四部分，其中I、II为正方形，III、IV为长方形，I、II的面积之和等于III、IV面积之和的2倍，若II的边长为2，且I的面积小于II的面积，则I的边长为（）

A、4 B、3 C、 $4 - 2 \sqrt{3}$ D、 $4 + 2 \sqrt{3}$

查看试题解析
11. 如图，AB是⊙O的直径，点E是AB上一点，过点E作CD⊥AB ，交⊙O于点C ， D ，以下结论正确的是（　　）

A、若⊙O的半径是2，点E是OB的中点，则CD＝ $\sqrt{3}$ B、若CD＝ $\sqrt{3}$ ，则⊙O的半径是1 C、若∠CAB＝30°，则四边形OCBD是菱形 D、若四边形OCBD是平行四边形，则∠CAB＝60°

查看试题解析
12. 如图，是二次函数y＝ax²+bx+c图象的一部分，其对称轴是x＝﹣1，且过点(﹣3，0)，下列说法：①abc＜0；②2a﹣b＝0；③若(﹣5，y₁)，(3，y₂)是抛物线上两点，则y₁＝y₂；④4a+2b+c＜0，其中说法正确的（）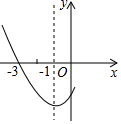

A、①② B、①②③ C、①②④ D、②③④

查看试题解析

二、填空题

13. 如果点P（x，y）关于原点的对称点为（1，3），则x +y＝．

查看试题解析
14. 已知点A为反比例函数y＝ $\frac{k}{x}$ 图象上的点，过点A分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为8，则k的值为．

查看试题解析
15. 某校欲从初三级部3名女生，2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛，则恰好选中一男一女的概率是．

查看试题解析
16. 已知一个圆心角为 $120 °$ 的扇形，半径为9，则以它为侧面围成的圆锥底面圆的半径为．

查看试题解析
17. 请写出一个开口向下，并且与y轴交于点（0，1）的抛物线的表达式

查看试题解析
18. 已知在直角坐标平面内，以点P（﹣3，4）为圆心，r为半径画圆，⊙P与坐标轴恰好有三个交点，那么r的取值是．

查看试题解析
19.
如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP= ．

查看试题解析
20. 如图，在直角坐标系中，正方形ABCD的顶点坐标分别为A(1，﹣1)，B(﹣1，﹣1)，C(﹣1，1)，D(1，1)．曲线AA₁A₂A₃…叫做“正方形的渐开线”，其中AA₁、A₁A₂、A₂A₃、A₃A₄…的圆心依次是B、C、D、A循环，则点A₁₈的坐标是．

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{x}{x - 3} - \frac{1}{3 - x}) \div \frac{x + 1}{x^{2} - 9}$ ，其中 $x$ 满足方程 $x^{2} - x - 6 = 0$ ．

查看试题解析
22. 如图，AB是⊙O的直径，CD是⊙O的弦，且CD⊥AB于点E.

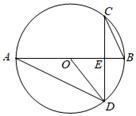(1)、求证：∠ADO＝∠C；

(2)、若⊙O的半径为5，BE＝2，求CD的长.

查看试题解析
23. RtΔABC中，∠C=90°，AC=8，BC=6，矩形CDEF的另三个顶点D、E、F均在RtΔABC的边上，且邻边之比为1：2，画出正确的图形，并直接写出矩形周长的值．

查看试题解析
24. 如图，已知抛物线 $y = x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ 两点．

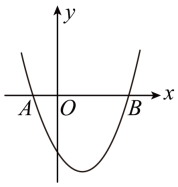(1)、求抛物线的解析式和顶点坐标；

(2)、点P为抛物线上一点，若 $S_{△ A B P} = 10$ ，求出此时点P的坐标．

查看试题解析
25. 平面内有一等腰直角三角板（∠ACB＝90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F．当点E与点A重合时（如图1），易证：AF+BF＝2CE．

(1)、当三角板绕点A顺时针旋转至图2的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．

(2)、当三角板绕点A顺时针旋转至图3的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．

查看试题解析
26. 某网商经销一种玩具，每件进价为40元．市场调查反映，每星期的销售量y（件）与销售单价x（元）之间的函数关系为y＝﹣10x+900（40≤x≤90）

(1)、如果该网商每个星期想获得4000元的利润，请你计算出玩具的销售单价定为多少元？

(2)、当每件玩具的销售价定为多少元时，该网商每星期经销这种玩具能够获得最大销售利润？最大销售利润是多少？（每件玩具的销售利润＝售价﹣进价）

查看试题解析
27. 如图，已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A$ 、 $B$ 两点， $A$ 点的坐标是 $(- 2 ， 1)$ ， $B$ 点的坐标是 $(1 ， n)$ ．

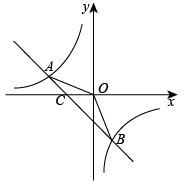(1)、求出两个函数解析式；

(2)、在 $x$ 轴正半轴上是否存在点 $P$ ，使 $△ A B P$ 为等腰三角形？若存在，求 $P$ 点坐标；若不存在，请说明理由．

查看试题解析