黑龙江省黑河市逊克县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1.
观察下列图形，既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 抛物线 $y = 2 {(x - 3)}^{2} + 1$ 的顶点坐标是（）

A、（3，1） B、（3，﹣1） C、（﹣3，1） D、（﹣3，﹣1）

查看试题解析
3. 点M(4，-3)关于原点对称的点N的坐标是（）

A、(-4，-3) B、(-4，3) C、(4，3) D、(-3，4)

查看试题解析
4. 下列事件中,必然事件是（）

A、打开电视,它正在播广告 B、掷两枚质地均匀的正方体骰子,点数之和一定大于6 C、早晨的太阳从东方升起 D、没有水分,种子发芽

查看试题解析
5. 一副扑克牌有54张，(黑桃、红桃、方片、草花各13张，大小王各一张)从牌中任意摸出一张牌是红桃的概率是（）

A、 $\frac{13}{52}$ B、 $\frac{13}{54}$ C、 $\frac{1}{2}$ D、 $\frac{13}{27}$

查看试题解析
6. 如果方程（m﹣3） $x^{m^{2} - 7}$ ﹣x+3=0是关于x的一元二次方程，那么m的值为（）

A、±3 B、3 C、﹣3 D、都不对

查看试题解析
7. 某药品经过两次降价，每瓶零售价由100元降为81元，已知两次降价的百分率相同，设每次降价的百分率为x，根据题意列方程得（）

A、100(1+x)²=81 B、100 (1-x²)=81 C、100(1-2x)=81 D、100(1-x)²=81

查看试题解析
8. 已知圆的半径为3，一点到圆心的距离是1，则这个点在（）

A、圆内 B、圆上 C、圆外 D、都有可能

查看试题解析
9. PA、PB分别切⊙O于A、B两点，C为⊙O上一动点(点C不与A、B重合)，∠APB=50°，则∠ACB=（）

A、100° B、115° C、65°或115° D、65°

查看试题解析
10. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，现有下列结论：①b²﹣4ac＞0 ②a＞0 ③b＞0 ④c＞0 ⑤9a+3b+c＜0，则其中结论正确的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. α，β是方程x²-2x-1=0的两根，则代数式α+β+αβ= ．

查看试题解析
12. 要在一只不透明的袋中放入若干个只有颜色不同的乒乓球，搅匀后，使得从袋中任意摸出一个乒乓球是白色的概率是 $\frac{1}{5}$ ，可以怎样放球：(只写一种即可)．

查看试题解析
13. 二次函数y=（x-1）²+2的最小值是．

查看试题解析
14. 已知 $x^{2} - 2 x = 5$ ，则代数式 $2 x^{2} - 4 x - 1$ 的值为．

查看试题解析
15. 如图，A、B、C为⊙O上三点，且∠OAB=64°，则∠ACB的度数是度．

查看试题解析
16. 一个母线长为6cm，底面半径为3cm的圆锥展开后得到的侧面展开图扇形的圆心角是度．

查看试题解析
17. 如图，△ABC中，∠CAB＝70°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得C′C//AB，则∠BAB′等于．

查看试题解析
18. 将一个正六边形绕着其中心，至少旋转度可以和原来的图形重合．

查看试题解析
19. 如图，⊙O的半径为2，弦AB= $2 \sqrt{3}$ ，点C是弦AB上一动点，OC长为整数，则OC的长为．

查看试题解析
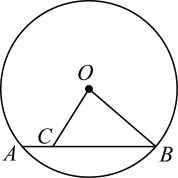20. 若某等腰三角形的三条边长都是一元二次方程 $x^{2} - 9 x = - 14$ 的根，则这个等腰三角形的周长是．

查看试题解析

三、解答题

21. 解下列方程：

(1)、 $x^{2} - 4 x - 12 = 0$ (用配方法)

(2)、 $y^{2} - 6 y = 7$

查看试题解析
22. 如图， $△ A B C$ 各顶点的坐标分别为A(4、4)，B(－2，2)，C(3，0)，

(1)、画出 $△ A B C$ 关于原点O对称的 $△ A^{'} B^{'} C^{'}$ ；

(2)、直接写出 $A^{'} ， B^{'} ， C^{'}$ 三点的坐标．

查看试题解析
23. 淘淘和明明玩骰子游戏，每人将一个各面分别标有1，2，3，4，5，6的正方体骰子掷一次，把两人掷得的点数相加，并约定：点数之和等于6，淘淘赢；点数之和等于7，明明赢；点数之和是其它数，两人不分胜负．

(1)、请你用“画树状图”或“列表”的方法分析说明此游戏是否公平．

(2)、请你基于（1）问中得到的数据，设计出一种公平的游戏规则．(列出一种即可)

查看试题解析
24. 如图1所示，将一个长为6宽为4的长方形ABEF，裁成一个边长为4的正方形ABCD和一个长为4、宽为2的长方形CEFD如图2．现将小长方形CEFD绕点C顺时针旋转至 $C E^{'} F^{'} D^{'}$ ，旋转角为a．

(1)、当点 $D^{'}$ 恰好落在EF边上时，求旋转角a的值；

(2)、如图3，G为BC中点，且0°＜a＜90°，求证： $G D^{^{'}} = E^{^{'}} D$ ；

(3)、小军是一个爱动手研究数学问题的孩子，他发现在小长方形CEFD绕点C顺时针旋转一周的过程中， $△ D C D^{'}$ 与 $△ C B D^{'}$ 存在两次全等，请你帮助小军直接写出当 $△ D C D^{'}$ 与 $△ C B D^{'}$ 全等时，旋转角a的值．

查看试题解析
25. 如图，AB是⊙O的直径，点D是AB延长线上的一点，点C在⊙O上，且AC＝CD，∠ACD＝120°.

(1)、求证：CD是⊙O的切线，

(2)、若⊙O的半径为3，求图中阴影部分的面积.

查看试题解析
26. 如图，抛物线y=-x²+bx+c与x轴交于A(2，0)，B(-6，0)两点．

(1)、求该抛物线的解析式；

(2)、若抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得 $△$ QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．

(3)、在坐标平面内是否存在一点P，使得Q、B、A、P围成的图形是平行四边形，若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析