黑龙江省鹤岗市绥滨县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x²﹣4=0的根是（）

A、x=2 B、x=﹣2 C、x₁=2，x₂=﹣2 D、x=4

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，∠A是⊙O的圆周角，∠A=40°，则∠BOC=（）

A、30° B、40° C、80° D、60°

查看试题解析
4. 下列事件是随机事件的是（　　）

A、每周有7天 B、袋中有三个红球，摸出一个球一定是红球 C、在同一平面内，垂直于同一条直线的两条直线互相垂直 D、任意购买一张车票，座位刚好靠窗口

查看试题解析
5. 已知关于x的一元二次方程ax²+bx+c=0有两个相等的实数根，则抛物线y=ax²+bx+c与x轴的交点个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 为了践行“绿水青山就是金山银山”的理念，某地计划将420亩荒山进行绿化，实际绿化时，工作效率是原计划的1.5倍，进而比原计划提前2天完成绿化任务，设原来平均每天绿化荒山 $x$ 亩，可列方程为（）

A、 $\frac{420}{x} - \frac{420}{1.5 x} = 2$ B、 $\frac{420}{x} + \frac{420}{1.5 x} = 2$ C、 $\frac{x}{420} - \frac{1.5 x}{420} = \frac{1}{2}$ D、 $\frac{x}{420} + \frac{1.5 x}{420} = \frac{1}{2}$

查看试题解析
7. 关于x的一元二次方程（m﹣1）x²+5x+m²﹣3m+2=0，常数项为0，则m值等于（）

A、1 B、2 C、1或2 D、0

查看试题解析
8. 已知二次函数y=-2（x+b）² ，当 $x < - 3$ 时，y随x的增大而增大，当 $x > - 3$ 时，y随x的增大而减小，则当 $x = 1$ 时，y的值为（）

A、-12 B、12 C、32 D、-32

查看试题解析
9. 如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是优弧 $\hat{A B C}$ 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（）

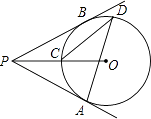A、15° B、20° C、25° D、30°

查看试题解析
10. 已知，如图，在 $△ A O B$ 中， $∠ A O B = 90 °$ ， $A O = 3$ cm， $B O = 4$ cm．将 $△ A O B$ 绕顶点O按顺时针方向旋转到 $△ A_{1} O B_{1}$ 处，此时线段 $O B_{1}$ 与AB的交点D恰好为AB的中点，则线段 $B_{1} D$ 的长是（）

A、1.5 cm B、3 cm C、5 cm D、2.5 cm

查看试题解析
11. 已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B₁在y轴上，点C₁、E₁、E₂、C₂、E₃、E₄、C₃在x轴上．若正方形A₁B₁C₁D₁的边长为1，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃ ，则点A₃到x轴的距离是（）．

A、 $\frac{3 + \sqrt{3}}{18}$ B、 $\frac{1 + \sqrt{3}}{18}$ C、 $\frac{3 + \sqrt{3}}{6}$ D、 $\frac{1 + \sqrt{3}}{6}$

查看试题解析

二、填空题

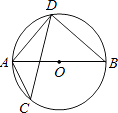
12. 抛物线y=-（x-2）²+2的顶点坐标是

查看试题解析
13. 若点 $A (- 3 ， y_{1})$ 、 $B (0 ， y_{2})$ 是二次函数 $y = - 2 (x - 1)^{2} + 3$ 图象上的两点，那么 $y_{1}$ 与 $y_{2}$ 的大小关系是（填 $y_{1} > y_{2}$ 、 $y_{1} = y_{2}$ 或 $y_{1} < y_{2}$ ）．

查看试题解析
14. 如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为

查看试题解析
15. 如果关于x的方程 $2 x^{2} - 3 x + k = 0$ 有两个相等的实数根，那么常数k的值为．

查看试题解析
16. 抛物线 $y = a x ² + b x + c$ 的顶点为 $D (- 1 ， 2)$ ，与x轴的一个交点A在点 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，其部分图象如图，则以下结论：① $b^{2} - 4 a c < 0$ ；② $a + b + c < 0$ ；③ $c - a = 2$ ；④方程 $a x^{2} + b x + c - 2 = 0$ 有两个相等的实数根．其中正确的结论有（填序号）．

查看试题解析
17. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是．

查看试题解析
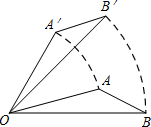18. 从﹣2，﹣1，2三个数中任取两个不同的数，作为点的坐标，则该点在第三象限的概率等于．

查看试题解析
19. 已知圆锥的母线长是10cm，侧面展开图的面积是60πcm² ，则这个圆锥的底面半径是cm．

查看试题解析
20. 某商店销售一种销售成本为40元/千克的水产品，若按50元/千克销售，一个月可售出500千克，销售价每涨价1元，月销售量就减少10千克，则月销售利润y（单位：元）与售价x（单位：元/千克）之间的函数解析式为

查看试题解析

三、解答题

21. 解方程

(1)、 $x (x - 2) + 3 (x - 2) = 0$ ；

(2)、 $x^{2} + 2 x - 1 = 0$ （配方法解方程）

查看试题解析
22. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．

⑴请画出将△ABC向下平移5个单位后得到的△A₁B₁C₁；

⑵将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A₂B₂C₂ ，并直接写出点B旋转到点B₂所经过的路径长．

查看试题解析
23. 如图，已知抛物线y＝ax²＋bx＋c与x轴交于点A（1，0），B（3，0），且过点C（0，－3）．

(1)、求抛物线的解析式；

(2)、若点P（4，m）在抛物线上，求△PAB的面积．

查看试题解析
24. 我市某中学举行“法制进校园”知识竞赛，赛后将学生的成绩分为A、B、C、D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图．请你根据统计图解答下列问题．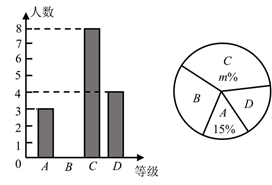

(1)、成绩为“B等级”的学生人数有名；

(2)、在扇形统计图中，表示“D等级”的扇形的圆心角度数为，图中m的值为；

(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛．已知“A等级”中有1名女生，请用列表或画树状图的方法求出女生被选中的概率．

查看试题解析
25. 如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．

(1)、求证：四边形ABFC是菱形；

(2)、若AD=7，BE=2，求半圆和菱形ABFC的面积．

查看试题解析
26. 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．

(1)、求每个月生产成本的下降率；

(2)、请你预测4月份该公司的生产成本．

查看试题解析
27. 如图，在等边△ABC中，点D为△ABC内的一点，∠ADB=120°，∠ADC=90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．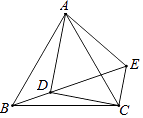

(1)、求证：AD=DE；

(2)、求∠DCE的度数；

(3)、若BD=1，求AD，CD的长．

查看试题解析
28. 超市销售某品牌洗手液，进价为每瓶10元.在销售过程中发现，每天销售量y（瓶）与每瓶售价x（元）之间满足一次函数关系（其中 $10 \leq x \leq 15$ ，且 $x$ 为整数），当每瓶洗手液的售价是12元时，每天销售量为90瓶；当每瓶洗手液的售价是14元时，每天销售量为80瓶.

(1)、求y与x之间的函数关系式；

(2)、设超市销售该品牌洗手液每天销售利润为w元，当每瓶洗手液的售价定为多少元时，超市销售该品牌洗手液每天销售利润最大，最大利润是多少元？

查看试题解析