广东省肇庆市封开县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，相反数最大的是（）

A、-5 B、-2 C、-1 D、0

查看试题解析
2. 习近平总书记提出了五年“精准扶贫”的战略构想，意味着每年要减贫约11600000人，将数据11600000用科学记数法表示为（）

A、 $1.16 \times 10^{6}$ B、 $1.16 \times 10^{7}$ C、 $1.16 \times 10^{8}$ D、 $11.6 \times 10^{6}$

查看试题解析
3. 在下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等腰三角形 B、平行四边形 C、正三角形 D、圆

查看试题解析
4. 如图所示，△ABC是⊙O的内接三角形．若∠ABC=70°，则∠AOC的度数等于（）

A、140° B、130° C、120° D、110°

查看试题解析
5. 抛物线y＝－2x²＋1的对称轴是（）

A、直线 $x= \frac{1}{2}$ B、直线 $x= - \frac{1}{2}$ C、y轴 D、直线x＝2

查看试题解析
6. 反比例函数y＝ $\frac{k - 1}{x}$ 的图象位于第二、四象限，则k的取值范围是（）

A、k≥1 B、k＞1 C、k＜1 D、k≤1

查看试题解析
7. 已知实数x，y满足|x−4|+（y−8）²＝0，则以x，y的值为两边长的等腰三角形的周长是（　　）

A、20或16 B、20 C、16 D、以上答案均不对

查看试题解析
8. 某校人工智能科普社团有12名成员，成员的年龄情况统计如下：
年龄（岁）
12
13
14
15
16
人数（人）
1
4
3
2
2
则这12名成员的平均年龄是（）

A、13岁 B、14岁 C、15岁 D、16岁

查看试题解析
9. 如图，抛物线y＝ax²＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b²；②方程ax²＋bx＋c＝0的两个根是x₁＝－1，x₂＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是（）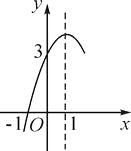

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 如图，已知EB是半圆⊙O的直径，A是BE延长线上一点，AC切半圆⊙O于点D，BC⊥AC于点C，DF⊥EB于点F，若BC＝2DF＝6，则⊙O的半径为（）

A、3.5 B、4 C、2 $\sqrt{3}$ D、3.75

查看试题解析

二、填空题

11. 计算：（ $\frac{1}{3}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣¹+ $\sqrt{(- 2)^{2}}$ ＝．

查看试题解析
12. 若关于x的一元二次方程 $x^{2} - 2 x + k = 0$ 有两个不相等的实数根，则k 的取值范围是.

查看试题解析
13. 在平面直角坐标系中，点 $(- 5 ， b)$ 关于原点对称的点为 $(a ， 6)$ ，则 $（ a ＋ b ）^{2022} ＝$ .

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， ∠ B = 22 ° ， P Q$ 垂直平分AB ，垂足为Q ，交BC于点P ．按以下步骤作图：以点A为圆心，以适当的长为半径作弧，分别交边AC ， AB于点D ， E；分别以点D ， E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧相交于点F；作射线AF ，射线AF与直线PQ相交于点G ，则 $∠ A G Q$ 的度数为度．

查看试题解析
15. 如图，反比例函数的图象与一次函数y＝﹣2x+3的图象相交于点P，点P到y轴的距离是1，则这个反比例函数的解析式是.

查看试题解析
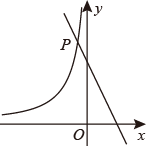16. 现有一个圆心角为 $120 °$ ，半径为6cm的扇形纸片，用它恰好围成一个圆锥的侧面，该圆锥底面圆的半径为cm．

查看试题解析
17. 如图，将△ABC沿其中位线DE翻折，点A落在BC边上的A′处．若BA′：A′C＝2：1，且△DB A′的面积为4，则△ABC的面积为．

查看试题解析

三、解答题

18. 解不等式组： ${\begin{array}{l} x - 1 > 0 \\ 2 x + 1 \leq 7 \end{array}$ ．

查看试题解析
19. 如图，在Rt△ABC，∠ABC＝90°，D、E分别是边BC，AC的中点，连接ED并延长到点F，使DF＝ED，连接BE、BF、CF、AD．求证：四边形BFCE是菱形．

查看试题解析
20. 化简求值： $\frac{x^{2} - 2 x + 1}{x^{2} - x}$ ÷（x﹣ $\frac{1}{x}$ ），其中x＝ $\sqrt{2}$ ．

查看试题解析
21. 为庆祝中国共产党成立100周年，某校举行党史知识竞赛活动，赛后随机抽取了部分学生的成绩，按得分划分为A，B，C，D[A等级（0≤x≤100），B等级（80≤x＜90），C等级（70≤x＜80），D等级（x＜70）]四个等级，并绘制了如下不完整的统计表和统计图．
根据图表信息，回答下列问题：

(1)、表中a＝；扇形统计图中，C等级所占的百分比是；D等级对应的扇形圆心角为度；若全校共有1800名学生参加了此次知识竞赛活动，请估计成绩为A等级的学生共有人．

(2)、若95分以上的学生有4人，其中甲、乙两人来自同一班级，学校将从这4人中随机选出两人参加市级比赛，请用列表或树状图法求甲、乙两人至少有1人被选中的概率．

查看试题解析
22. 如图，在矩形OABC中，AB＝4，BC＝8，点D是边AB的中点，反比例函数 $y = \frac{k}{x}$ （x＞0）的图象经过点D，交BC边于点E．

(1)、求反比例函数 $y = \frac{k}{x}$ （x＞0）的解析式和E点坐标；

(2)、连结DE，在y轴上找一点P，使△PDE的周长最小，求出此时P的坐标．

查看试题解析
23. 某商场计划购进A、B两种新型台灯共80盏，它们的进价与售价如下表所示：
类型价格
进价（元/盏）
售价（元/盏）
A型
30
45
B型
50
70

(1)、若商场预计进货款为2900元，则这两种台灯各购进多少盏?

(2)、若商场规定B型台灯的进货数量不超过A型台灯进货数量的4倍，应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?

查看试题解析
24. 如图，AB是⊙O的直径，AC是弦，P为AB延长线上一点，∠BCP＝∠BAC，∠ACB的平分线交⊙O于点D，交AB于点E，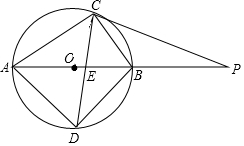

(1)、求证：PC是⊙O的切线；

(2)、求证：△PEC是等腰三角形；

(3)、若AC＋BC＝2时，求CD的长．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于A，B两点，与y轴交于C点，OA=1，OB=OC=3．

(1)、求抛物线的表达式；

(2)、如图1，点D为第一象限抛物线上一动点，连接DC，DB，BC，设点D的横坐标为m，△BCD的面积为S，求S的最大值；

(3)、如图2，点P(0，n)是线段OC上一点(不与点O、C重合)，连接PB，将线段PB以点P为中心，旋转90°得到线段PQ，是否存在n的值，使点Q落在抛物线上？若存在，请求出满足条件的n的值，若不存在，请说明理由．

查看试题解析

类型价格	进价（元/盏）	售价（元/盏）
A型	30	45
B型	50	70

年龄（岁）	12	13	14	15	16
人数（人）	1	4	3	2	2