广东省韶关市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列生态环保标志中,是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 已如⊙O的半径等于3,圈心O到直线l的距离为5,那么直线l与⊙O的位置关系是 ( )A、直线l与⊙O相交 B、直线l与⊙O相离 C、直线l与⊙O相切 D、无法确定3. 文明出行,遵守交通规则“红灯停,绿灯行”,一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是绿灯的概率是( )A、 B、 C、 D、4. 抛物线与轴的一个交点是(一1,0),那么抛物线与轴的另一个交点坐标是( )A、(0,0) B、(3,0) C、(-3,0) D、(0,-3)5. 如图,直线l与半径为5cm的⊙O相交于A、B两点,且与半径OC垂直,垂足为H.若AB=8cm,l要与⊙O相切,则l应沿OC所在直线向下平移( )
2. 已如⊙O的半径等于3,圈心O到直线l的距离为5,那么直线l与⊙O的位置关系是 ( )A、直线l与⊙O相交 B、直线l与⊙O相离 C、直线l与⊙O相切 D、无法确定3. 文明出行,遵守交通规则“红灯停,绿灯行”,一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是绿灯的概率是( )A、 B、 C、 D、4. 抛物线与轴的一个交点是(一1,0),那么抛物线与轴的另一个交点坐标是( )A、(0,0) B、(3,0) C、(-3,0) D、(0,-3)5. 如图,直线l与半径为5cm的⊙O相交于A、B两点,且与半径OC垂直,垂足为H.若AB=8cm,l要与⊙O相切,则l应沿OC所在直线向下平移( )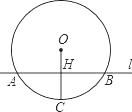 A、1cm B、2cm C、3cm D、4cm6. 如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC长等于( )
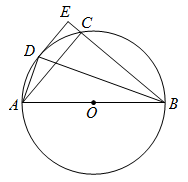
A、1cm B、2cm C、3cm D、4cm6. 如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC长等于( )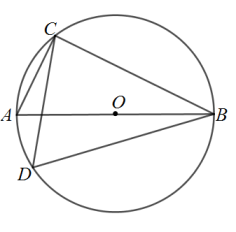 A、8 B、10 C、 D、7. 如图,将△ABC绕点A顺时针旋转60°得到△AED.若线段AB=3,则BE=( )
A、8 B、10 C、 D、7. 如图,将△ABC绕点A顺时针旋转60°得到△AED.若线段AB=3,则BE=( )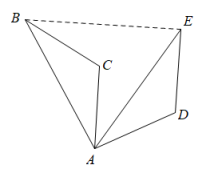 A、2 B、3 C、4 D、58. 如图,一边靠墙(墙有足够长),其它三边用12 m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是( )
A、2 B、3 C、4 D、58. 如图,一边靠墙(墙有足够长),其它三边用12 m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是( ) A、16 m2 B、12 m2 C、18 m2 D、以上都不对9. 某网店销售一批运动装,平均每天可销售20套,每套盈利45元;为扩大销售量,增加盈利,采取降价措施,一套运动服每降价1元,平均每天可多卖4套,若网店要获利2100元,设每套运动装降价元,则列方程正确的是( )A、 B、 C、 D、10. 二次函数的图象如图所示,下列说法正确的是( )
A、16 m2 B、12 m2 C、18 m2 D、以上都不对9. 某网店销售一批运动装,平均每天可销售20套,每套盈利45元;为扩大销售量,增加盈利,采取降价措施,一套运动服每降价1元,平均每天可多卖4套,若网店要获利2100元,设每套运动装降价元,则列方程正确的是( )A、 B、 C、 D、10. 二次函数的图象如图所示,下列说法正确的是( )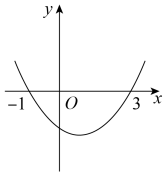 A、 B、 C、 D、当时,函数有最小值
A、 B、 C、 D、当时,函数有最小值二、填空题
-
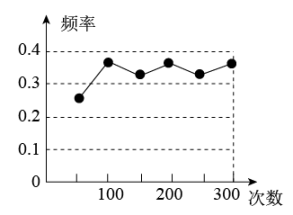
11. 已知点和点关于原点对称,则 .12. 关于的方程有一个根是3,那么实数的值是13. 一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的概率稳定在0.2,则袋中有绿球个.14. 圆锥的侧面积为 , 底面半径为6,则圆锥的母线长为 .15. 如图,为某小组做“用频率估计概率”的实验时,绘制的频率折线图,则符合这一结果的实验是 . (填写序号)
①抛一枚硬币,出现正面朝上;
②掷一个正六面体的骰子,出现3点朝上;
③一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃;
④从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球.
 16. 如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .
16. 如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .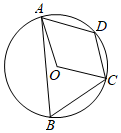 17. 如图,在等腰直角三角形ABC中,AB=BC=2cm,以直角顶点B为圆心,AB长为半径画弧,再以AC为直径画弧,两弧之间形成阴影部分.阴影部分面积为cm2 .
17. 如图,在等腰直角三角形ABC中,AB=BC=2cm,以直角顶点B为圆心,AB长为半径画弧,再以AC为直径画弧,两弧之间形成阴影部分.阴影部分面积为cm2 .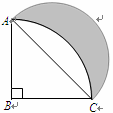
三、解答题
-
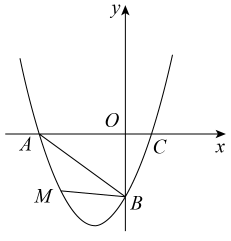
18. 如图,已知点A(0,0),B(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB'C'.
 (1)、画出△AB'C';(2)、求的长度.19. 举世瞩目的港珠澳大桥已于2018年10月24日正式通车,这座大桥是世界上最长的跨海大桥,被誉为“新世界七大奇迹”,车辆经过这座大桥收费站时,从已开放的4个收费通道、、、中可随机选择其中一个通过.(1)、一辆车经过收费站时,选择通道通过的概率是 .(2)、用树状图或列表法求两辆车经过此收费站时,选择不同通道通过的概率.20. 为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为100万元,2020年12月该企业口罩出口订单额为121万元.(1)、求该企业2020年10月到12月口罩出口订单额的月平均增长率;(2)、按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额能否达到140万元?21. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.
(1)、画出△AB'C';(2)、求的长度.19. 举世瞩目的港珠澳大桥已于2018年10月24日正式通车,这座大桥是世界上最长的跨海大桥,被誉为“新世界七大奇迹”,车辆经过这座大桥收费站时,从已开放的4个收费通道、、、中可随机选择其中一个通过.(1)、一辆车经过收费站时,选择通道通过的概率是 .(2)、用树状图或列表法求两辆车经过此收费站时,选择不同通道通过的概率.20. 为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为100万元,2020年12月该企业口罩出口订单额为121万元.(1)、求该企业2020年10月到12月口罩出口订单额的月平均增长率;(2)、按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额能否达到140万元?21. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.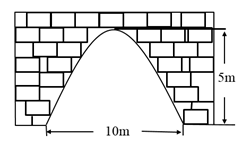
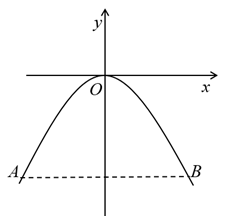 (1)、建立如图的直角坐标系,求抛物线的解析式;(2)、一艘货船宽8m,水面两侧高度2m,能否安全通过此桥?22. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)、建立如图的直角坐标系,求抛物线的解析式;(2)、一艘货船宽8m,水面两侧高度2m,能否安全通过此桥?22. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.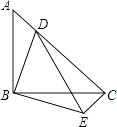 (1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.
(1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.