广东省清远市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²+2x-1＝0中，下列说法错误的是（）

A、二次项系数是1 B、一次项系数是2 C、一次项是2x D、常数项是1

查看试题解析
2. 下列命题中正确的是（）

A、一对邻角互补的四边形是平行四边形 B、矩形的对角线互相垂直平分 C、一组对边平行且一组对角相等的四边形是平行四边形 D、菱形的对角线相等

查看试题解析
3. 如图，l₁∥l₂∥l₃ ， DE＝6，EF＝7，AB＝5，则BC的长为（）

A、 $\frac{35}{6}$ B、 $\frac{9}{4}$ C、4 D、6

查看试题解析
4. 有两组卡片，第一组卡片上写有a，b，b，第二组卡片上写有a，b，b，c，c，求从每组卡片中各抽出一张，都抽到b的概率是（）

A、 $\frac{4}{15}$ B、 $\frac{8}{15}$ C、 $\frac{1}{2}$ D、 $\frac{4}{9}$

查看试题解析
5.
下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序正确的是（　　）

A、A⇒B⇒C⇒D B、D⇒B⇒C⇒A C、C⇒D⇒A⇒B D、A⇒C⇒B⇒D

查看试题解析
6. 如图所示的物体由两个紧靠在一起的圆柱体组成，它的左视图是（）

A、 B、 C、 D、

查看试题解析
7. 小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）

A、矩形 B、菱形 C、正方形 D、长方形

查看试题解析
8. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，配方结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
9. 如图，在平面直角坐标系中，将 $△ O A B$ 以原点O为位似中心放大后得到 $△ O C D$ ，若 $B (0 ， 1)$ ， $D (0 ， 3)$ ，则 $△ O A B$ 与 $△ O C D$ 的相似比是（）

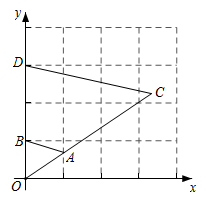A、2：1 B、1：2 C、3：1 D、1：3

查看试题解析
10. 如图，把含30°的直角三角板PMN放置在正方形ABCD中， $∠ P M N = 30 °$ ，直角顶点P在正方形ABCD的对角线BD上，点M，N分别在AB和CD边上，MN与BD交于点O，且点O为MN的中点，则 $∠ A M P$ 的度数为（）

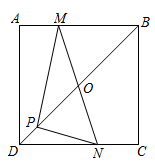A、60° B、65° C、75° D、80°

查看试题解析

二、填空题

11. 若两个相似三角形的相似比为3∶4，则它们的面积比为．

查看试题解析
12. 如果 $(m + 3) x^{2} - m x + 1 = 0$ 是一元二次方程，则m的取值范围是.

查看试题解析
13. 如图，点P把线段AB分成两部分，且BP、AP、AB、BP是成比例线段．如果AB＝1，那么BP＝．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (1 ， 2)$ 和点 $B (- 1 ， m)$ ，则 $m$ 的值为．

查看试题解析
15. 某班同学开展“50人中有2个人的生日相同”的试验活动．每个同学课外调查20个人的生日，然后从全班的调查结果中随机选取50个被调查人的生日，记录其中有无2个人的生日相同．每选取50个被调查人的生日为一次试验，经过重复多次试验，部分数据记录如下（保留两位小数）：
试验的总次数
50
100
150
200
250
…
“有2个人的生日相同”的次数
45
97
144
194
242
…
“有2个人的生日相同”的频率
▲
0.97
0.96
0.97
▲
…
请根据上表中的数据，估计“50人中有2个人的生日相同”的概率是．

查看试题解析
16. 如图，在菱形ABCD中，对角线 $A C = 12$ ， $B D = 16$ ，分别以点A，B，C，D为圆心， $\frac{1}{2} A B$ 的长为半径画弧，与该菱形的边相交，则图中阴影部分的面积为.（结果保留 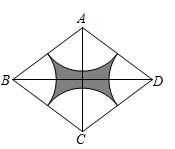$π$ ）

查看试题解析
17. 如图，经过原点O的直线与反比例函数 $y = \frac{a}{x}$ （a＞0）的图象交于A，D两点（点A在第一象限），点B，C，E在反比例函数 $y = \frac{b}{x}$ （b＜0）的图象上，AB∥y轴，AE∥CD∥x轴，五边形ABCDE的面积为56，四边形ABCD的面积为32，则a－b的值为．

查看试题解析

三、解答题

18. 小敏与小霞两位同学解方程

3 (x - 3) = {(x - 3)}^{2}

的过程如下框：

小敏：

两边同除以 $(x - 3)$ ，得

$3 = x - 3$ ，

则 $x = 6$ ．

小霞：

移项，得 $3 (x - 3) - {(x - 3)}^{2} = 0$ ，

提取公因式，得 $(x - 3) (3 - x - 3) = 0$ ．

则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ ，

解得 $x_{1} = 3$ ， $x_{2} = 0$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

19. 如图，在Rt△ABC中，∠C=90°，D是AC边上的一点，DE⊥AB于点E．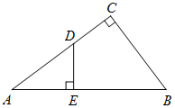

(1)、求证：△ABC∽△ADE；

(2)、如果AC=4，BC=3，DE=2，求AD的长．

查看试题解析
20. 某果园有100棵桃树，一棵桃树平均结1000个桃子，现准备多种一些桃树以提高产量，试验发现，每多种一棵桃树，每棵树的产量就会减少2个，但多种的桃树不能超过100棵，如果要使产量增加15.2%，那么应多种多少棵桃树？

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 m x + 3 m^{2} = 0$ ．

(1)、求证：该方程总有两个实数根；

(2)、若 $m > 0$ ，且该方程的两个实数根的差为2，求 $m$ 的值．

查看试题解析
22. 某气球内充满一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．

(1)、求这个函数的表达式及写出变量V的取值范围；

(2)、当气体体积为1m³时，气压是多少？

(3)、当气球内的气压大于128kPa时，气球将爆炸，为了安全考虑，气体的体积应不小于多少？

查看试题解析
23. 晚上，李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图，当李明走到点A处时，张龙测得李明直立时身高AM与其影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得 $A B = 1.2 m$ .已知李明直立时的身高为 $1.6 m$ ，求路灯的高CD的长.

查看试题解析
24. 小明根据学习函数的经验对y＝﹣1＋ $\frac{1}{x}$ 的图象的性质进行了探究．下面是小明的探究过程，请补充完整．

(1)、函数y＝﹣1＋ $\frac{1}{x}$ 的自变量x取值范围为；

(2)、完成表格，并画出函数的图象（答题卡已给出平面直角坐标系）；
x
…
－3
－2
－1
$- \frac{1}{2}$
$- \frac{1}{3}$
$\frac{1}{3}$
$\frac{1}{2}$
1
2
3
…
y
…
$- \frac{4}{3}$
$- \frac{3}{2}$
－2
－3
2
1
0
$- \frac{1}{2}$
…

(3)、根据图象写出函数y＝﹣1＋ $\frac{1}{x}$ 的两条性质．

查看试题解析
25. 如图，

(1)、【推理】
如图1，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G.
求证： $△ B C E ≌ △ C D G$ .

(2)、【运用】
如图2，在（推理）条件下，延长BF交AD于点H.若 $\frac{H D}{H F} = \frac{4}{5}$ ， $C E = 9$ ，求线段DE的长.

(3)、【拓展】
将正方形改成矩形，同样沿着BE折叠，连结CF，延长CF，BF交直线AD于G，两点，若 $\frac{A B}{B C} = k$ ， $\frac{H D}{H F} = \frac{4}{5}$ ，求 $\frac{D E}{E C}$ 的值（用含k的代数式表示）.

查看试题解析

试验的总次数	50	100	150	200	250	…
“有2个人的生日相同”的次数	45	97	144	194	242	…
“有2个人的生日相同”的频率	▲	0.97	0.96	0.97	▲	…