广东省梅州市平远县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 2sin60°的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 下面性质中矩形具有而菱形没有的是（）

A、对角线相等 B、邻边相等 C、对角线垂直 D、对边相等

查看试题解析
3. 若x₁、x₂是一元二次方程x²＋9x＋20＝0的两个根，则x₁＋x₂的值是（）

A、﹣9 B、9 C、20 D、﹣20

查看试题解析
4. 两个位似图形中，对应点到位似中心的线段比为 $2 ： 3$ ，则这两个图形的面积比为（）

A、2：3 B、4：9 C、 $\sqrt{2} ： \sqrt{3}$ D、1：2

查看试题解析
5. 在一个不透明的袋子中，装有红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同．若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在 $0.15$ ．和 $0.45$ ，则该袋子中的白色球可能有(　　)

A、6个 B、16个 C、18个 D、24个

查看试题解析
6. 同一时刻，小明在阳光下的影长为2米，与他邻近的旗杆的影长为6米，小明的身高为1.6米，则旗杆的高为（　　）

A、3.2米 B、4.8米 C、5.2米 D、5.6米

查看试题解析
7. 若点（0，a），（4，b）都在二次函数 $y = x^{2} - 4 x + 4$ 的图象上，则a与b的大小关系是（）

A、 $a > b$ B、 $a < b$ C、 $a = b$ D、无法确定

查看试题解析
8. 点D、E分别在△ABC的边AB、AC上，可推出DE $∥$ BC的条件是（）

A、 $\frac{B D}{A D} = \frac{4}{3} ， \frac{A E}{E C} = \frac{4}{3}$ B、 $\frac{A D}{A B} = \frac{2}{3} ， \frac{E C}{A E} = \frac{2}{3}$ C、 $\frac{A B}{A D} = \frac{4}{3} ， \frac{E C}{A E} = \frac{4}{3}$ D、 $\frac{A D}{A B} = \frac{2}{3} ， \frac{A E}{E C} = 2$

查看试题解析
9. 如图，四边形OABC和四边形BDEF都是正方形，反比例函数 $y = \frac{k}{x}$ 在第一象限的图像经过点E，若两正方形的面积差为12，则k的值为（）

A、12 B、6 C、10 D、8

查看试题解析
10. 如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB于E，点G是AE中点且∠AOG=30°，则下列结论正确的个数为（　　）
①△OGE是等边三角形；②DC=3OG；③OG= $\frac{1}{2}$ BC；④ $S_{Δ A O E} = \frac{1}{6} S_{矩形 A B C D}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 比较大小：tan50° tan60°．

查看试题解析
12. 若 $x ： y ： z = 3 ： 5 ： 6$ ，且 $3 y = 2 z + 3$ ，则 $x + 2 y + z$ 的值为．

查看试题解析
13. 抛物线 $y = (x + 2)^{2} + 3$ 上的点到x轴最短的距离是．

查看试题解析
14. 如图，E是正方形 $A B C D$ 的对角线 $B D$ 上任意一点，四边形 $E F C G$ 是矩形，若正方形 $A B C D$ 的边长为n，则矩形 $E F C G$ 的周长为．

查看试题解析
15. 将长为4cm的线段进行黄金分割，则较短的线段是cm．

查看试题解析
16. 从数﹣3， $- \frac{3}{2}$ ， 0，2中任取一个数记为a，再从余下的三个数中，任取一个数记为b．若k＝a+b，反比例函数y＝ $\frac{k}{x}$ 的图象经过第一、三象限的概率是．

查看试题解析
17. 某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙长20米），另外三边用篱笆围成如图所示，所用的篱笆长为32米．请问当垂直于墙的一边的长为米时，花圃的面积有最大值，最大值是．

查看试题解析

三、解答题

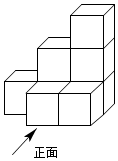
18. 如图，是由几个大小完全相同的小正方体垒成的几何体，请分别画出你所看到的几何体的三视图．

查看试题解析
19. 为巩固防疫成果，确保校园平安，某市所有学校都严格落实测体温进校园的防控要求．某校开设了A、B、C三个测温通道，某天早晨，该校小亮和小丽两位同学将随机通过测温通道进入校园，利用画树状图或列表的方法，求小亮和小丽从同一个测温通道通过的概率．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - 4 x + 2 m = 0$ 有两个不相等的实数根，如果m为非负整数，且该方程的根都是整数，求m的值及此时方程的根．

查看试题解析
21. 如图，小东在教学楼距地面9m高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°.

(1)、求旗杆AB的高.（结果精确到0.01m，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

(2)、升旗时，国旗上端悬挂在距地面2.25m处.若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x - 3 a$ 与x轴负半轴交于点A（－1，0），与x轴的另一交点为B，与y轴正半轴交于点C（0，3），抛物线的对称轴与直线BC相交于点M，与x轴交于点G．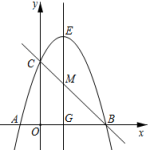

(1)、求抛物线的解析式及对称轴；

(2)、抛物线的对称轴上存在点P，且点P在x轴上方时，满足∠APB=∠ABC，求PG的长．

查看试题解析
23. 如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(2)、当AD，AB满足什么条件时，四边形MENF是正方形．

查看试题解析
24. 如图1，在平面直角坐标系中，直线AB与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点A (1，3)和点B (3， n)，与x轴交于点C，与y轴交于点D．

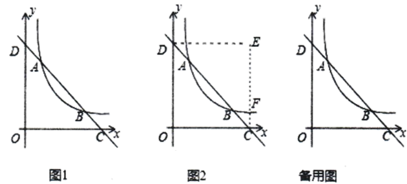(1)、求反比例函数的表达式及n的值；

(2)、将△OCD沿直线AB翻折，点O落在第一象限内的点E处， EC与反比例函数的图象交于点F．
①请求出点F的坐标；

②在x轴上是否存在点P，使得△DPF是以DF为斜边的直角三角形?若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
25. 如图，已知四边形ABCD中，AB⊥AD，BC∥AD，E为AB的中点，且EC、ED分别为∠BCD、∠ADC的角平分线，EF⊥CD交BC的延长线于点G，连接DG.

(1)、求证：CE⊥DE；

(2)、若AB=6，求CF·DF的值；

(3)、当△BCE与△DFG相似时， $\frac{BC}{A D}$ 的值是.

查看试题解析