广东省茂名市茂南区2021-2022学年九年级上学期期末数学试题2

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个实数中，无理数是（）

A、 $\sqrt{2}$ B、-0.3333 C、 $\frac{22}{7}$ D、 $\sqrt[3]{8}$

查看试题解析
2. 若 $\sqrt{3 x - 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x$ ≤ $\frac{1}{3}$ B、 $x$ ≥ $\frac{1}{3}$ C、 $x$ ﹥0 D、 $x$ <-1

查看试题解析
3. 已知2a=3b，则下列比例式错误的是（）

A、 $\frac{3}{a}$ = $\frac{2}{b}$ B、 $\frac{a}{3}$ = $\frac{b}{2}$ C、 $\frac{b}{a}$ = $\frac{2}{3}$ D、 $\frac{2}{a}$ = $\frac{3}{b}$

查看试题解析
4. 某校为了解九年级学生的视力情况，从九年级的800名学生中随机抽查200名学生进行视力检测，下列说法正确的是（）

A、800名学生是总体 B、200名学生是个体 C、200名学生是总体的一个样本 D、200是样本容量

查看试题解析
5. 在平面直角坐标系中，点P(x²＋1，－2)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，在矩形ABCD中，对角线AC，BD交于点O，下列条件：①AC⊥BD，②AB=BC，③∠ACB=45°，④OA=OB．上述条件能使矩形ABCD是正方形的是（）

A、①②③④ B、①②③ C、②③④ D、①③④

查看试题解析
7. 已知（x-1）²=2，则代数式 $x^{2} -$ 2 $x$ +5的值为（）

A、4 B、5 C、6 D、7

查看试题解析
8. 直线y= $x$ +a不经过第四象限，则关于 $x$ 的方程a $x^{2}$ -2 $x$ -1=0的实数解的个数是（）

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
9. 如图，点A、B、C是⊙O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O于点F，则∠BAF等于(　　)

A、12.5° B、15° C、20° D、22.5°

查看试题解析
10. 如图，已知二次函数y=ax²+bx+c给出下列结论：①abc＜0，②4a+2b+c＜0，③a+c＞b，④a+b≤t（at+b）（t是任意一个实数），⑤当x＜-1时，y随x的增大而减少．其中结论正确的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 分解因式： $x^{2}$ －9= ．

查看试题解析
12. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
13. 若单项式 $a^{2} b^{m + 1}$ 与 $\frac{1}{3} a^{n}$ b的和仍是单项式，则 $n^{m}$ 的值是．

查看试题解析
14. 已知三角形三边长分别为1，3， $x$ ，若 $x$ 为奇数，则 $x$ 值为．

查看试题解析
15. 二次函数y=x²+2x+1先向右平移2个单位长度，再向下平移3个单位长度得到的解析式为．

查看试题解析
16. 如图，矩形ABCD中，AB=4，AD=6，动点E在矩形的边AB上运动，连接DE，作点A关于DE的对称点P，连接BP，则BP的最小值为．

查看试题解析
17. 如图，在平面直角坐标系中，动点P从原点O出发，水平向左平移1个单位长度，再竖直向下平移1个单位长度得到点 $P_{1} (- 1 ， - 1)$ ；接着水平向右平移2个单位长度，再竖直向上平移2个单位长度得到点 $P_{2}$ ；接着水平向左平移3个单位长度，再竖直向下平移3个单位长度得到点 $P_{3}$ ；接着水平向右平移4个单位长度，再竖直向上平移4个单位长度得到点 $P_{4}$ ， …，按此作法进行下去，则点 $P_{2022}$ 的坐标为．

查看试题解析

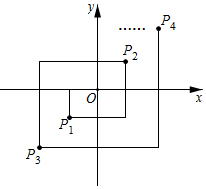
三、解答题

18. 计算： ${(π - 2021)}^{0} - 3 \tan 30 ° + | 1 - \sqrt{3} | + {(\frac{1}{2})}^{- 2}$ ．

查看试题解析
19. 如图，在△ABC中．

(1)、作边BC的垂直平分线交边AB于点D，交BC于点E，（保留作图痕迹，不写作法）

(2)、连接CD，若D是AB的中点，试判断△ABC的形状，并说明理由．

查看试题解析
20. 为了培养学生成为具有“社会责任、学术素养、创新能力、国际视野”的未来人才，我校提出“让每一个孩子成长为一棵参天大树”的“树”课程理念，数学科开发了四门“树”课程供学生选择：A.趣味数学；B.棋海巡航；C.中外数学史；D.数独与幻方.某年级共有100名学生选择了A课程，为了解本年级选择A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制）分成六组，绘制成频数分布直方图.

(1)、该年级学生小李随机选取了一门课程，则小李选中课程C的概率是；

(2)、根据题中信息，估计该年级选择A课程学生成绩在80≤x＜90的总人数是；

(3)、该年级每名学生选两门不同的课程，小张和小王在选课程的过程中，若第一次都选了课程C.那么他俩第二次同时选择课程A或课程B的概率是多少？请用列表法或树状图的方法加以说明.

查看试题解析
21. 如图，点B（4，a）是反比例函数y $= \frac{12}{x} (x > 0)$ 图象上一点，过点B分别向坐标轴作垂线，垂足为A，C．反比例函数y $= \frac{k}{x} (x > 0)$ 的图象经过OB的中点M，与AB，BC分别相交于点D，E．连接DE并延长交 $x$ 轴于点F，连接BF．

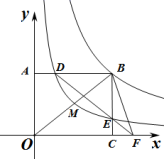(1)、求k的值；

(2)、求△BDF的面积．

查看试题解析
22. 为了做好新冠疫情的防控工作，某超市计划购进A，B两种消毒液出售，A种消毒液比B种消毒液每瓶进价少3元，已知用1600元购进的A种消毒液的数量是1100元购进的B种消毒液数量的2倍．

(1)、求A，B两种消毒液每瓶进价各是多少元？

(2)、疫情进入了防控常态，该超市老板决定用不超过1960元购进A、B两种消毒液共200瓶，已知A种消毒液售价为14元，B种消毒液售价为18元，请设计出该超市售完该批消毒液后获得最大利润的购进方案，并求出最大利润．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D是 $B C$ 边的中点，连接 $A D$ ，分别过点A，C作 $A E ∥ B C$ ， $C E ∥ A D$ 交于点E，连接 $D E$ ，交 $A C$ 于点O．

(1)、求证：四边形 $A D C E$ 是矩形；

(2)、若 $A B = 10$ ， $\sin ∠ C O E = \frac{4}{5}$ ，求 $C E$ 的长．

查看试题解析
24. 如图，△ABC是以AB为直径的⊙O的内接三角形，BD与⊙O相切于点B，与AC的延长线交于点D，E是BD的中点，CE交BA的延长线于点F，BD＝8，BE $= \frac{1}{3}$ EF．

(1)、求证：FC是⊙O的切线；

(2)、求AF的长；

(3)、若∠F= $20 °$ ， BC=3 $\sqrt{2}$ ，求图中阴影部分的面积．

查看试题解析
25. 如图，抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于A（-1，0），B（3，0）两点，与y轴交于点C，直线 $y = - x + 3$ 经过B，C两点，连接AC．

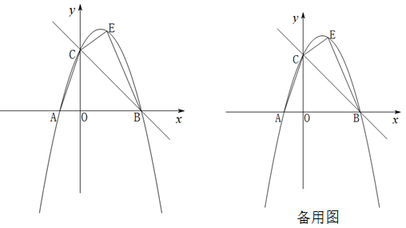(1)、求抛物线的表达式；

(2)、点E为直线BC上方的抛物线上的一动点（点E不与点B，C重合），连接BE，CE，设四边形BECA的面积为S，求S的最大值；

(3)、若点Q在 $x$ 轴上，则在抛物线上是否存在一点P，使得以B，C，P，Q四点为顶点的四边形是平行四边形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

查看试题解析