广东省江门台山市2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列交通标志是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
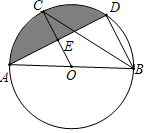
D、 2. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、投掷一枚质地均匀的骰子,掷得的点数是奇数 C、等腰三角形的两个底角相等 D、 是实数,3. 若关于x的一元二次方程()的一个解是 , 则的值是( )A、2021 B、2020 C、2019 D、20184. 将抛物线y= x2向左平移一个单位,所得抛物线的解析式为( )A、y= x2+1 B、y= x2﹣1 C、y= (x+1)2 D、y= (x﹣1)25. 已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )A、 B、 C、 D、6. 圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切7. 台山某学校某个宿舍同学毕业时都将自己的照片向全宿舍其他同学各送一张表示留念,全宿舍共送56张照片,设该宿舍共有x名同学,根据题意,列出方程为( )A、 B、 C、 D、8. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为 的直径,弦 ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
2. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、投掷一枚质地均匀的骰子,掷得的点数是奇数 C、等腰三角形的两个底角相等 D、 是实数,3. 若关于x的一元二次方程()的一个解是 , 则的值是( )A、2021 B、2020 C、2019 D、20184. 将抛物线y= x2向左平移一个单位,所得抛物线的解析式为( )A、y= x2+1 B、y= x2﹣1 C、y= (x+1)2 D、y= (x﹣1)25. 已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )A、 B、 C、 D、6. 圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切7. 台山某学校某个宿舍同学毕业时都将自己的照片向全宿舍其他同学各送一张表示留念,全宿舍共送56张照片,设该宿舍共有x名同学,根据题意,列出方程为( )A、 B、 C、 D、8. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为 的直径,弦 ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )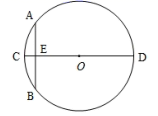 A、12寸 B、13寸 C、24寸 D、26寸9. 如图,将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,连接AC、EG,取AC、EG的中点M、N,连接MN,若AB=8,BC=6,则MN=( )
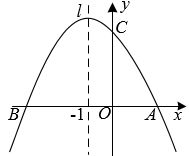
A、12寸 B、13寸 C、24寸 D、26寸9. 如图,将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,连接AC、EG,取AC、EG的中点M、N,连接MN,若AB=8,BC=6,则MN=( )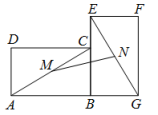 A、8 B、6 C、5 D、10. 如图,抛物线 与x轴交于点(3,0),对称轴为直线x=1.结合图象分析下列结论:① ;② ;③一元二次方程 的两根分别为 ;④ .其中正确的结论有( )个
A、8 B、6 C、5 D、10. 如图,抛物线 与x轴交于点(3,0),对称轴为直线x=1.结合图象分析下列结论:① ;② ;③一元二次方程 的两根分别为 ;④ .其中正确的结论有( )个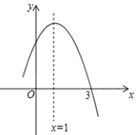 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知点A(a,1)与点A′(5,b)是关于原点对称,则a+b =.12. 若某扇形花坛的面积为6m2 , 半径为3m,则该扇形花坛的弧长为m.13. 表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n
200
500
800
2000
5000
12000
成活的棵数m
187
446
730
1790
4510
10836
成活的频率
0.935
0.892
0.913
0.895
0.902
0.903
由此估计这种苹果树苗移植成活的概率约为(精确到0.1)
14. 已知正六边形的边长为2,则它的内切圆的半径为 .15. 如图, ABC的内切圆与三边分别相切于点D、E、F,若∠B=50°,则∠EDF=度.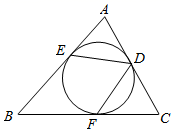 16. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形的边有公共点,则实数a的取值范围是 .
16. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形的边有公共点,则实数a的取值范围是 .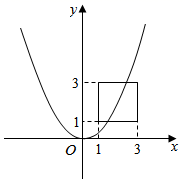 17. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=4,BC=9,以A为旋转中心将腰AB顺时针旋转90°至AE,连接DE,若DE=DB,则△ADE的面积等于 .
17. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=4,BC=9,以A为旋转中心将腰AB顺时针旋转90°至AE,连接DE,若DE=DB,则△ADE的面积等于 .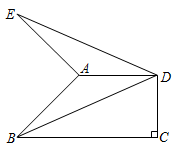
三、解答题
-
18. 解方程:19. 如图,△OPQ是边长为2的等边三角形,若反比例函数(k为常数且)的图象经过点P,求该反比例函数的解析式.
 20. 如图,已知抛物线经过A(-3,0)、C(0,-3)两点.
20. 如图,已知抛物线经过A(-3,0)、C(0,-3)两点.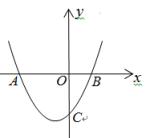 (1)、求b,c的值;(2)、求抛物线与x轴的另一个交点B的坐标,并结合图象,写出当时,x的取值范围.21. 甲、乙两人分别从A、B、C这3个景点随机选择2个景点游览.(1)、求甲选择的2个景点是A、B的概率.(2)、甲、乙两人选择的2个景点恰好相同的概率是.22. 如图, 中, , , ,一动点P从点C出发沿着 方向以 的速度运动,另一动点Q从A出发沿着 边以 的速度运动,P,Q两点同时出发,运动时间为 .
(1)、求b,c的值;(2)、求抛物线与x轴的另一个交点B的坐标,并结合图象,写出当时,x的取值范围.21. 甲、乙两人分别从A、B、C这3个景点随机选择2个景点游览.(1)、求甲选择的2个景点是A、B的概率.(2)、甲、乙两人选择的2个景点恰好相同的概率是.22. 如图, 中, , , ,一动点P从点C出发沿着 方向以 的速度运动,另一动点Q从A出发沿着 边以 的速度运动,P,Q两点同时出发,运动时间为 . (1)、若 的面积是 面积的 ,求t的值?(2)、△PCQ的面积能否为 面积的一半?若能,求出t的值;若不能,说明理由.23. 如图,D、E、F是Rt△ABC三边上的点,且四边形CDEF为矩形,BC=6, .
(1)、若 的面积是 面积的 ,求t的值?(2)、△PCQ的面积能否为 面积的一半?若能,求出t的值;若不能,说明理由.23. 如图,D、E、F是Rt△ABC三边上的点,且四边形CDEF为矩形,BC=6, .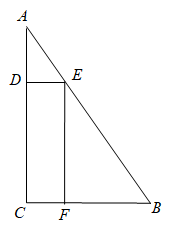 (1)、求AB的长;(2)、设 , 则DE= . EF=(用含x的表达式表示).(3)、求矩形CDEF的面积的最大值.
(1)、求AB的长;(2)、设 , 则DE= . EF=(用含x的表达式表示).(3)、求矩形CDEF的面积的最大值.