广东省惠州市仲恺高新区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列成语所描述的事件是随机事件的是( )A、瓮中捉鳖 B、守株待兔 C、水涨船高 D、水中捞月3. 已知的半径为 , 若直线与的圆心O的距离 , 则直线与的位置关系是( )A、相交 B、相切 C、相离 D、外离4. 若两个相似三边形的周长之比为 , 则它们的面积之比为( )A、 B、 C、 D、5. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、k≥0 B、k≤0 C、k<0且 D、k≤0且6. 如图,已知圆心角的度数为 , 则圆周角的度数是( )
2. 下列成语所描述的事件是随机事件的是( )A、瓮中捉鳖 B、守株待兔 C、水涨船高 D、水中捞月3. 已知的半径为 , 若直线与的圆心O的距离 , 则直线与的位置关系是( )A、相交 B、相切 C、相离 D、外离4. 若两个相似三边形的周长之比为 , 则它们的面积之比为( )A、 B、 C、 D、5. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、k≥0 B、k≤0 C、k<0且 D、k≤0且6. 如图,已知圆心角的度数为 , 则圆周角的度数是( )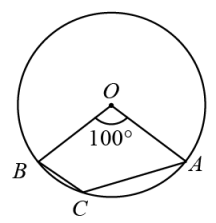 A、 B、 C、 D、7. 抛物线的图象如图所示,那么( )
A、 B、 C、 D、7. 抛物线的图象如图所示,那么( ) A、 , , B、 , , C、 , , D、 , ,8. 如图,排水管截面的半径为5分米,水面宽分米, , 则水的最大深度CD为( )
A、 , , B、 , , C、 , , D、 , ,8. 如图,排水管截面的半径为5分米,水面宽分米, , 则水的最大深度CD为( )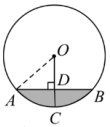 A、 B、 C、 D、9. 已知 , 则是函数和的图象大致是( )A、
A、 B、 C、 D、9. 已知 , 则是函数和的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
10. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( ) A、
A、 B、
B、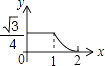 C、
C、 D、
D、
二、填空题
-
11. 若反比例函数的图象过点 , 则k= .12. 二次函数的顶点坐标是 .13. 在某一时刻,测得一根高为2m的竹竿的影长为1m,同时测得一栋建筑物的影长为12m,那么这栋建筑物的高度为m.14. 设 , , 是抛物线上的三点,则用“”表示 , , 的大小关系为 .15. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接AD,若 ,则 .
 16. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为 . (结果保留π)
16. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为 . (结果保留π) 17. 如图,已知:是的直径,弦 , 分别过 , 作的垂线,垂足为 , . 得到如下结论:①;②;③若四边形是正方形,则;④若为的中点,则为中点;⑤若半径 , 则扇形的面积为;所有正确结论的序号是 .
17. 如图,已知:是的直径,弦 , 分别过 , 作的垂线,垂足为 , . 得到如下结论:①;②;③若四边形是正方形,则;④若为的中点,则为中点;⑤若半径 , 则扇形的面积为;所有正确结论的序号是 .
三、解答题
-
18. 解方程:19. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上.
 (1)、画出绕原点按逆时针方向旋转后的;(2)、求点旋转到点所经过的路线长(结果保留).20. 甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.(1)、请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;(2)、若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.21. 在国家的宏观调控下,某市的商品房成交价由去年10月份的14000元/ 下降到12月份的11340元/ .(1)、求11、12两月份平均每月降价的百分率是多少?(2)、如果房价继续回落,按此降价的百分率,你预测到今年2月份该市的商品房成交均价是否会跌破10000元/ ?请说明理由22. 如图,一次函数与反比例函数的图象相交于A,B两点,且与坐标轴的交点为 , , 点B的横坐标为-4.
(1)、画出绕原点按逆时针方向旋转后的;(2)、求点旋转到点所经过的路线长(结果保留).20. 甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.(1)、请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;(2)、若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.21. 在国家的宏观调控下,某市的商品房成交价由去年10月份的14000元/ 下降到12月份的11340元/ .(1)、求11、12两月份平均每月降价的百分率是多少?(2)、如果房价继续回落,按此降价的百分率,你预测到今年2月份该市的商品房成交均价是否会跌破10000元/ ?请说明理由22. 如图,一次函数与反比例函数的图象相交于A,B两点,且与坐标轴的交点为 , , 点B的横坐标为-4.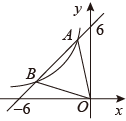 (1)、试确定反比例函数的解析式;(2)、求的面积;(3)、直接写出不等式的解.23. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)、试确定反比例函数的解析式;(2)、求的面积;(3)、直接写出不等式的解.23. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. (1)、求证:DE是⊙O的切线.(2)、求DE的长.24. 如图,在中, , , . 点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、分别从、同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为秒.
(1)、求证:DE是⊙O的切线.(2)、求DE的长.24. 如图,在中, , , . 点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、分别从、同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为秒. (1)、当为何值时,的面积等于?(2)、当为何值时,的长度等于?(3)、探究经过多少秒后,以点 , , 为顶点的三角形与相似?25. 如图,直线与轴,轴分别交于点 , , 抛物线经过 , 两点,与轴的另一交点为 , 点是抛物线上一动点.
(1)、当为何值时,的面积等于?(2)、当为何值时,的长度等于?(3)、探究经过多少秒后,以点 , , 为顶点的三角形与相似?25. 如图,直线与轴,轴分别交于点 , , 抛物线经过 , 两点,与轴的另一交点为 , 点是抛物线上一动点.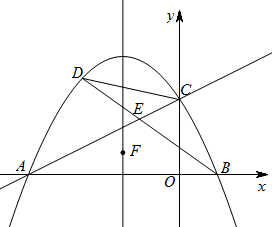 (1)、求抛物线的解析式;(2)、当点在直线上方时,连接 , , , 交于点 , 令的面积为 , 的面积为 , 求的最大值;(3)、点是该抛物线对称轴上一动点,是否存在以点 , , , 为顶点的平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当点在直线上方时,连接 , , , 交于点 , 令的面积为 , 的面积为 , 求的最大值;(3)、点是该抛物线对称轴上一动点,是否存在以点 , , , 为顶点的平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.