广东省惠州市惠城区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
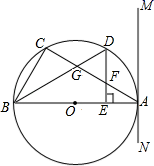
D、 2. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>13. 对于二次函数y=2(x﹣2)2+1,下列说法中正确的是( )A、图象的开口向下 B、函数的最小值为1 C、图象的对称轴为直线x=﹣2 D、图象的顶点坐标是(1,2)4. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、155. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
2. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>13. 对于二次函数y=2(x﹣2)2+1,下列说法中正确的是( )A、图象的开口向下 B、函数的最小值为1 C、图象的对称轴为直线x=﹣2 D、图象的顶点坐标是(1,2)4. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、155. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、6. 若正三角形的周长为12,则这个正三角形的边心距为( )A、 B、 C、 D、7. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、8. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,若∠DEF=52°,则∠A的度数是( )
A、 B、 C、 D、6. 若正三角形的周长为12,则这个正三角形的边心距为( )A、 B、 C、 D、7. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、8. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,若∠DEF=52°,则∠A的度数是( )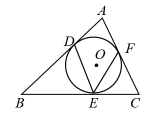 A、52° B、76° C、26° D、128°9. 定义:如果一元二次方程满足 , 那么我们称这个方程为“蜻蜓”方程.已知关于的方程是“蜻蜓”方程,且有两个相等的实数根,则下列结论中一定正确的是( )A、 B、 C、 D、10. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(2,0),其对称轴是直线x=﹣1,直线y=3恰好经过顶点.有下列判断:①当x<﹣2时,y随x增大而减小; ②ac<0; ③a﹣b+c<0; ④方程ax2+bx+c=0的两个根是x1=2,x2=﹣4;⑤当m≤3时,方程ax2+bx+c=m有实数根.其中正确的是( )
A、52° B、76° C、26° D、128°9. 定义:如果一元二次方程满足 , 那么我们称这个方程为“蜻蜓”方程.已知关于的方程是“蜻蜓”方程,且有两个相等的实数根,则下列结论中一定正确的是( )A、 B、 C、 D、10. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(2,0),其对称轴是直线x=﹣1,直线y=3恰好经过顶点.有下列判断:①当x<﹣2时,y随x增大而减小; ②ac<0; ③a﹣b+c<0; ④方程ax2+bx+c=0的两个根是x1=2,x2=﹣4;⑤当m≤3时,方程ax2+bx+c=m有实数根.其中正确的是( )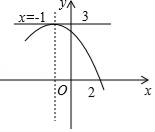 A、①②③ B、①②④ C、②④⑤ D、②③④
A、①②③ B、①②④ C、②④⑤ D、②③④二、填空题
-
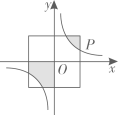
11. 已知点A(a,1)与点B(4,b)关于原点对称,则a-b= .12. 二次函数y=(x+4)2+1的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为 .13. 若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2012﹣2a﹣2b的值 .14. 点P(﹣1,m﹣3)在第三象限,则反比例函数y=的图象在第象限.15. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .16. 如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,P(2a,a)是反比例函数y=的图象与正方形的边的一个交点,则图中阴影部分的面积是 .
 17. 如图,在扇形BOC中,∠BOC=60°,OD 平分∠BOC交弧BC于点D . 点E为半径OB 上一动点,若 OB=2 ,则阴影部分周长的最小值为 .
17. 如图,在扇形BOC中,∠BOC=60°,OD 平分∠BOC交弧BC于点D . 点E为半径OB 上一动点,若 OB=2 ,则阴影部分周长的最小值为 .
三、解答题
-
18. 解方程: .19. 有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.(1)、请用树状图或列表的方法求这三条线段能组成三角形的概率;(2)、求这三条线段能组成直角三角形的概率.20. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上.
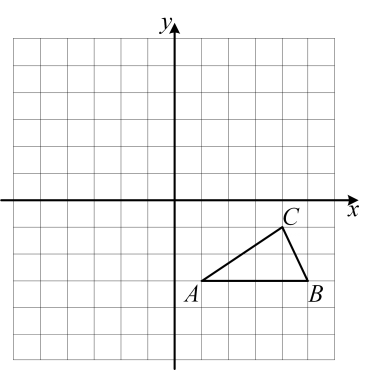
⑴画出 关于原点对称的;
⑵画出向上平移5个单位后的 , 并求出平移过程中线段扫过的面积.
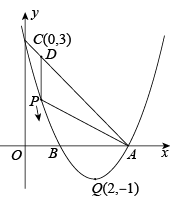
21. 某汽车销售公司2017年10月份销售一种新型低能耗汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.(1)、求11月份和12月份的平均增长率;(2)、该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂队销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2018年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)22. 如图,在正方形ABCD内有一点P,且PA= , BP= , PC=1.若将绕点逆时针旋转90°后,得到 . (1)、求的长;(2)、∠BPC度数.23. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 .
(1)、求的长;(2)、∠BPC度数.23. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 . (1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.
(1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.