广东省河源市紫金县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程，是一元二次方程的是（）

A、 $x^{2} + 3 x - 1 = 0$ B、 $y^{2} - 5 x = 1$ C、 $2 x + 1 = 0$ D、 $\frac{1}{x} + x^{2} = 1$

查看试题解析
2. 下面几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 若△ABC∽△DEF，且△ABC与△DEF的面积比是 $\frac{9}{4}$ ，则△ABC与△DEF的对应高的比为（）

A、 $\frac{2}{3}$ B、 $\frac{81}{16}$ C、 $\frac{9}{4}$ D、 $\frac{3}{2}$

查看试题解析
4. 若正方形的对角线长为2 cm，则这个正方形的面积为（）

A、4cm² B、2cm² C、 $\sqrt{2}$ cm² D、2 $\sqrt{2}$ cm²

查看试题解析
5. 下表记录了一名球员在罚球线上投篮的结果，这么球员投篮一次，投中的概率约是（）
投篮次数
10
50
100
150
200
250
300
500
投中次数
4
35
60
78
104
123
152
251
投中频率
0.40
0.70
0.60
0.52
0.52
0.49
0.51
0.50

A、0.7 B、0.6 C、0.5 D、0.4

查看试题解析
6. 如图，点A为反比例函数 $y = \frac{k}{x}$ 的图象上一点，过A作AB⊥x轴于点B ，连接OA ，已知△ABO的面积为3，则k值为（）．

A、-3 B、3 C、-6 D、6

查看试题解析
7. 如图，线段 $A B$ 两个端点的坐标分别为 $A (2 ， 2) 、 B (2.5 ， 0.8)$ ，以原点O为位似中心，在第一象限内将线段 $A B$ 扩大为原来的2倍后得到线段 $C D$ ，则端点C的坐标为（）

A、 $(3 ， 1.6)$ B、 $(4 ， 3.2)$ C、 $(4 ， 4)$ D、 $(6 ， 1.6)$

查看试题解析
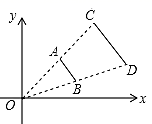8. 由于疫情得到缓和，餐饮行业逐渐回暖，某地一家餐厅重新开张，开业第一天收入约为5000元，之后两天的收入按相同的增长率增长，第3天收入约为6050元，若设每天的增长率为x，则x满足的方程是（）

A、5000（1+x）＝6050 B、5000（1+2x）＝6050 C、5000（1﹣x）²＝6050 D、5000（1+x）²＝6050

查看试题解析
9. 如图，正比例函数 $y_{1} = k_{1} x$ 的图像与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象相交于A、B两点，其中点A的横坐标为2，当 $y_{1} > y_{2}$ 时，x的取值范围是（）

A、x＜-2或x＞2 B、x＜-2或0＜x＜2 C、-2＜x＜0或0＜x＜2 D、-2＜x＜0或x＞2

查看试题解析
10. 如图，正方形 $A B C D$ 中， $E$ 为 $B C$ 中点，连接 $A E$ ， $D F ⊥ A E$ 于点 $F$ ，连接 $C F$ ， $F G ⊥ C F$ 交 $A D$ 于点 $G$ ，下列结论：① $C F = C D$ ；② $G$ 为 $A D$ 中点；③ $Δ D C F ~ Δ A G F$ ；④ $\frac{A F}{E F} = \frac{2}{3}$ ，其中结论正确的个数有（）

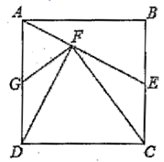A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 方程 $x^{2} = x$ 的解是．

查看试题解析
12. 若关于x的一元二次方程ax²+4x﹣2＝0有实数根，则a的取值范围为 .

查看试题解析
13. 一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗，每次随机摸出一颗珠子，放回摇匀后再摸，通过多次试验发现摸到白珠子的频率稳定在0.3左右，则盒子中黑珠子可能有颗．

查看试题解析
14. 已知矩形ABCD，当满足条件时，它成为正方形（填一个你认为正确的条件即可）．

查看试题解析
15. 反比例函数y= $\frac{k}{x}$ 的图象经过点（1，﹣2），则k的值为．

查看试题解析
16. 如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段 $A C$ 的长为．

查看试题解析
17. 如图，正方形纸片ABCD的边长为12，E，F分别是边AD，BC上的点，将正方形纸片沿EF折叠，使得点A落在CD边上的点A′处，此时点B落在点B′处．已知折痕EF=13，则AE的长等于．

查看试题解析

三、解答题

18. 解方程：2x²﹣4x﹣1＝0．

查看试题解析
19. 如图，在△ABC中，AB=AC，BD=CD，CE⊥AB于E．求证：△ABD∽△CBE．

查看试题解析
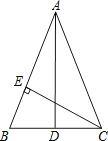20. 如图，小明站在路灯B下的A处，向前走5米到D处，发现自己在地面上的影子DC是2米．若小明的身高DE是1.8米，则路灯B离地面的高度AB是多少米？

查看试题解析
21. 如图，已知矩形ABCD的两条对角线相交于点O，∠ACB＝30°，AB＝2．

(1)、求AC的长及∠AOB的度数；

(2)、以OB，OC为邻边作菱形OBEC，求菱形OBEC的面积．

查看试题解析
22. 如图，一条直线上有两只蚂蚁，甲蚂蚁在点A处，乙蚂蚁在点B处，假设两只蚂蚁同时出发，爬行方向只能沿直线AB在“向左”或“向右”中随机选择，并且甲蚂蚁爬行的速度比乙蚂蚁快.

(1)、甲蚂蚁选择“向左”爬行的概率为；

(2)、利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.

查看试题解析
23. 有一块长60m，宽50m的矩形荒地，地方政府准备在此建一个综合性休闲广场，其中黑色部分为通道，通道的宽度均相等，中间的三个矩形（其中三个矩形的一边长均为am）区域将铺设塑胶地面作为运动场地．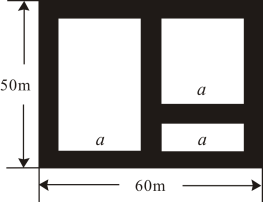

(1)、设通道的宽度为xm，则a＝（用含x的代数式表示）；

(2)、若塑胶运动场地总的占地面积为2430m² ，则通道的宽度为多少？

查看试题解析
24. 已知，如图，正比例函数y＝ax的图象与反比例函数图象交于A点（3，2），

(1)、试确定上述正比例函数和反比例函数的表达式．

(2)、根据图象回答：在第一象限内，当反比例函数值大于正比例函数值时x的取值范围？

(3)、M（m，n）是反比例函数上一动点，其中0大于m小于3，过点M作直线MN平行x轴，交y轴于点B．过点A作直线AC平行y轴，交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

查看试题解析
25. 如图1，在平面直角坐标系中，已知直线l：y＝kx+b与x轴交于点A，与y轴交于点B，与直线CD相交于点D，其中AC＝14，C（﹣6，0），D（2，8）．

(1)、求直线l的函数解析式；

(2)、如图2，点P为线段CD延长线上的一点，连接PB，当△PBD的面积为7时，将线段BP沿着y轴方向平移，使得点P落在直线AB上的P'处，求点P′到直线CD的距离；

(3)、若点E为直线CD上的一点，则在平面直角坐标系中是否存在点F，使以点A，D，E，F为顶点的四边形为菱形？若存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．

查看试题解析

投篮次数	10	50	100	150	200	250	300	500
投中次数	4	35	60	78	104	123	152	251
投中频率	0.40	0.70	0.60	0.52	0.52	0.49	0.51	0.50