广东省河源市和平县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 下列命题是真命题的是( )A、四个角都相等的四边形是菱形 B、四条边都相等的四边形是正方形 C、平行四边形、菱形、矩形都既是轴对称图形,又是中心对称图形 D、顺次连接菱形各边中点得到的四边形是矩形2. 如图,该几何体的俯视图是( )
 A、
A、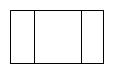 B、
B、 C、
C、 D、
D、 3. 如图,直线AB//CD//EF,若BD:DF=3:4,AC=3.6,则AE的长为( )
3. 如图,直线AB//CD//EF,若BD:DF=3:4,AC=3.6,则AE的长为( ) A、4.8 B、6.6 C、7.6 D、8.44. 已知在Rt△ABC中,∠C=90°,若sinA= , 则cosA等于( )A、 B、 C、 D、15. 若关于x的一元二次方程有两个实数根,则实数k的取值范围是( ).A、 B、 C、且 D、且6. 一个封闭的箱子中有两个红球和一个黄球,随机从中摸出两个球,即两个球均为红球的概率是( )A、 B、 C、 D、7. 已知正比例函数y1=kx的图象与反比例函数y2= 的图象相交于点A(2,4),则下列说法正确的是( )A、正比例函数y1与反比例函数y2都随x的增大而增大 B、两个函数图象的另一交点坐标为(2,﹣4) C、当x<﹣2或0<x<2时,y1<y2 D、反比例函数y2的解析式是y2=﹣8. 如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B= , E为边AC的中点,则 cos∠ADE的值为( )
A、4.8 B、6.6 C、7.6 D、8.44. 已知在Rt△ABC中,∠C=90°,若sinA= , 则cosA等于( )A、 B、 C、 D、15. 若关于x的一元二次方程有两个实数根,则实数k的取值范围是( ).A、 B、 C、且 D、且6. 一个封闭的箱子中有两个红球和一个黄球,随机从中摸出两个球,即两个球均为红球的概率是( )A、 B、 C、 D、7. 已知正比例函数y1=kx的图象与反比例函数y2= 的图象相交于点A(2,4),则下列说法正确的是( )A、正比例函数y1与反比例函数y2都随x的增大而增大 B、两个函数图象的另一交点坐标为(2,﹣4) C、当x<﹣2或0<x<2时,y1<y2 D、反比例函数y2的解析式是y2=﹣8. 如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B= , E为边AC的中点,则 cos∠ADE的值为( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF 的面积为2,则△ABC的面积为( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF 的面积为2,则△ABC的面积为( ) A、8 B、10 C、12 D、1410. 如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,AD=6,则BE的长为( )
A、8 B、10 C、12 D、1410. 如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,AD=6,则BE的长为( ) A、 B、 C、3 D、3.5
A、 B、 C、3 D、3.5二、填空题
-
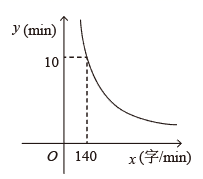
11. 方程x2=2x的解是.12. 高为7米的旗杆在水平地面上的影子长为5米,同一时刻测得附近一个建筑物的影子长30米,则此建筑物的高度为米.13. 小明要把一篇文章录入电脑,所需时间 与录入文字的速度 (字 )之间的反比例函数关系如图所示,如果小明要在 内完成录入任务,则小明录入文字的速度至少为字 .
 14. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为.
14. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为.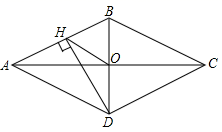 15. 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30角时,已知两次测量的影长相差8米,则树高AB为多少? . (结果保留根号)
15. 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30角时,已知两次测量的影长相差8米,则树高AB为多少? . (结果保留根号) 16. 如图,在平面直角坐标系中,△ABC和△A1B1C1是以坐标原点O为位似中心的位似图形,且点B(5,1),B1(10,2),若△ABC的面积为m,则△A1B1C1的面积为 .
16. 如图,在平面直角坐标系中,△ABC和△A1B1C1是以坐标原点O为位似中心的位似图形,且点B(5,1),B1(10,2),若△ABC的面积为m,则△A1B1C1的面积为 . 17. 如图,点 , 在反比例函数的图象上,点 , 在反比例函数的图像上,轴,已知点 , 的横坐标分别为2,4,与的面积之和为3,则的值为 .
17. 如图,点 , 在反比例函数的图象上,点 , 在反比例函数的图像上,轴,已知点 , 的横坐标分别为2,4,与的面积之和为3,则的值为 .
三、解答题
-
18. 解方程:3x2+5(2x+1)=0.19. 如图,CD是线段AB的垂直平分线,M是AC延长线上一点.
 (1)、用直尺和圆规:作∠BCM的角平分线CN,过点B作CN的垂线,垂足为E;(保留作图痕迹,不要求写作法)(2)、求证:四边形BECD是矩形.20. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.(1)、请用列表或画树状图的方法表示出所有(m,n)可能的结果;(2)、若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?21. 已知如图,AD是ABC的中线,且 , E为AD上一点, .
(1)、用直尺和圆规:作∠BCM的角平分线CN,过点B作CN的垂线,垂足为E;(保留作图痕迹,不要求写作法)(2)、求证:四边形BECD是矩形.20. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.(1)、请用列表或画树状图的方法表示出所有(m,n)可能的结果;(2)、若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?21. 已知如图,AD是ABC的中线,且 , E为AD上一点, . (1)、求证:;(2)、若 , , 试求线段AD的长.22. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).
(1)、求证:;(2)、若 , , 试求线段AD的长.22. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号). 23. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米,
23. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米, (1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54米,那么小路的宽度是多少米?
(1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54米,那么小路的宽度是多少米?

