广东省东莞市虎门镇2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-10-11 类型:期末考试
一、单选题
-
1. 在有理数2,0,﹣1,﹣3中,任意取两个数相加,和最小是( )A、2 B、﹣1 C、﹣3 D、﹣42. 下列属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 从2021年5月26日在南昌召开的第十二届中国卫星导航年会上获悉,至2020年,我国卫星导航产业总值突破4000亿元,年均增长 以上,其中4000亿用科学记数法表示为( )A、 B、 C、 D、4. 若一个多边形的内角和等于720°,则这个多边形的边数是( )A、5 B、6 C、7 D、85. 函数中,自变量x的取值范围是( )A、 B、 C、 D、6. 如果数据 , , , 的方差是3,则另一组数据 , , , 的方差是( )A、3 B、6 C、12 D、57. 若 ,则 的值是( )A、5 B、-5 C、1 D、-18. 如图,把△ABC绕着点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( )
3. 从2021年5月26日在南昌召开的第十二届中国卫星导航年会上获悉,至2020年,我国卫星导航产业总值突破4000亿元,年均增长 以上,其中4000亿用科学记数法表示为( )A、 B、 C、 D、4. 若一个多边形的内角和等于720°,则这个多边形的边数是( )A、5 B、6 C、7 D、85. 函数中,自变量x的取值范围是( )A、 B、 C、 D、6. 如果数据 , , , 的方差是3,则另一组数据 , , , 的方差是( )A、3 B、6 C、12 D、57. 若 ,则 的值是( )A、5 B、-5 C、1 D、-18. 如图,把△ABC绕着点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( ) A、10° B、30° C、40° D、70°9. P为⊙O内一点, ,⊙O半径为5,则经过P点的最短弦长为( )A、5 B、6 C、8 D、1010. 二次函数的图象如图,对称轴为直线 , 关于的一元二次方程(为实数)在的范围内有解,则的取值范围是( )
A、10° B、30° C、40° D、70°9. P为⊙O内一点, ,⊙O半径为5,则经过P点的最短弦长为( )A、5 B、6 C、8 D、1010. 二次函数的图象如图,对称轴为直线 , 关于的一元二次方程(为实数)在的范围内有解,则的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 分解因式: .13. 小红参加学校举办的“我爱我的祖国”主题演讲比赛,她的演讲稿、语言表达、形象风度得分分别为85分,70分,80分,若依次按照40%,30%,30%的百分比确定成绩,则她的平均成绩是分.14. 在平面直角坐标系中,一次函数 与反比例函数 的图象交于 , 两点,则 的值是.15. 不等式组的解集为 .16. 如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A、C分别在x轴、y轴的正半轴上,点B的坐标为(1,2),若点P是第一象限内的一点,且∠OPC=45°,则线段AP最长时的P点坐标为.
 17. 如图所示,正方形的边长为1,其面积标记为 , 以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , …,按照此规律继续下去,则的值为 .
17. 如图所示,正方形的边长为1,其面积标记为 , 以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , …,按照此规律继续下去,则的值为 .
三、解答题
-
18. 化简:19. 如图,四边形是矩形.
 (1)、尺规作图:在边上求作点E,使得;(保留作图痕迹,不写作法)(2)、在(1)的条件下, , 求.20. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)、尺规作图:在边上求作点E,使得;(保留作图痕迹,不写作法)(2)、在(1)的条件下, , 求.20. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)21. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?22. 如图, 中, , ,点 、 分别在边 、 上,且 .
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)21. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?22. 如图, 中, , ,点 、 分别在边 、 上,且 .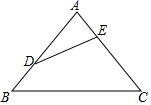 (1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.23. 如图,已知双曲线和直线交于点A和B,B点的坐标是 , 垂直y轴于点C, .
(1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.23. 如图,已知双曲线和直线交于点A和B,B点的坐标是 , 垂直y轴于点C, . (1)、求双曲线和直线的解析式;(2)、若 , 求的值.
(1)、求双曲线和直线的解析式;(2)、若 , 求的值.

