浙江省舟山市金衢山五校联盟2022-2023学年九年级上学期9月监测数学试题卷
试卷更新日期:2022-10-11 类型:月考试卷
一、选择题(本大题共10小题,每小题3分.)
-
1. 下列事件是必然事件的是( )A、任意一个三角形,它的内角和等于180° B、打开电视机,正在播放广告 C、掷一枚硬币,正面朝上 D、明天太阳从西方升起2. 二次函数的图像的对称轴是( )A、直线 B、直线 C、直线 D、直线3. 抛物线的顶点坐标( )A、(-4,1) B、(-4,-1) C、(4,-1) D、(4,1)4. 一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是必然事件的是( )A、3个球都是黑球 B、3个球都是白球 C、3个球中有黑球 D、3个球中有白球5. 已知⊙O的半径为2cm,点P到圆心O的距离为4cm,则点P和⊙O的位置关系为( )A、点P在圆内 B、点P在圆外 C、点P在圆上 D、不能确定6. 在同一直角坐标系中,函数和函数(a是常数,且a≠0)的图象可能是( )A、
 B、
B、 C、
C、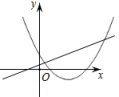 D、
D、 7. 抛物线的图象向左平移2个单位,再向上平移3个单位,所得图象的解析式为( )A、 B、 C、 D、8. 如图,正方形ABCD内接于⊙O,若随意抛出一粒石子在这个圆面上,则石子落在正方形ABCD内概率是( )
7. 抛物线的图象向左平移2个单位,再向上平移3个单位,所得图象的解析式为( )A、 B、 C、 D、8. 如图,正方形ABCD内接于⊙O,若随意抛出一粒石子在这个圆面上,则石子落在正方形ABCD内概率是( )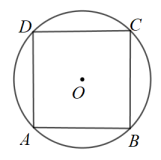 A、 B、 C、 D、9. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( ) A、(a,a) B、 C、 D、10. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图像如图所示,给出以下判断:①且;②;③;④;⑤直线与抛物线两个交点的横坐标分别为 , 则 . 其中正确的个数有( )
A、(a,a) B、 C、 D、10. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图像如图所示,给出以下判断:①且;②;③;④;⑤直线与抛物线两个交点的横坐标分别为 , 则 . 其中正确的个数有( ) A、1个 B、3个 C、5个 D、2个
A、1个 B、3个 C、5个 D、2个二、填空题(本题有6小题,每小题4分,共24分)
-
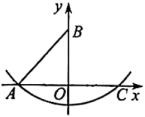
11. 如图,在平面直角坐标系中,点的坐标为 , 点在轴正半轴上,以点为圆心,长为半径作弧,交轴正半轴于点 , 则点的坐标为 .
 12. 如图:麻将是中国的国粹之一,玩法最为复杂有趣,是中国古人发明的一种博弈游戏.它开局拿牌要投两枚骰子,将两枚骰子的点数相加之和除以4看余数来决定是在哪家开始拿牌.余数为1则在自家拿牌,余数为2就在下家拿牌,余数为3则在对家拿牌,能被4整除就在上家拿牌,则在自家拿牌的概率为 .
12. 如图:麻将是中国的国粹之一,玩法最为复杂有趣,是中国古人发明的一种博弈游戏.它开局拿牌要投两枚骰子,将两枚骰子的点数相加之和除以4看余数来决定是在哪家开始拿牌.余数为1则在自家拿牌,余数为2就在下家拿牌,余数为3则在对家拿牌,能被4整除就在上家拿牌,则在自家拿牌的概率为 .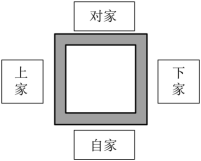 13. 已知函数在上有最大值4,则常数的值为.14. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”).
13. 已知函数在上有最大值4,则常数的值为.14. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”). 15. 把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6厘米,DC=7厘米.把三角板DCE绕点C顺时针旋转15°得到 , 如图(2),这时AB与相交于点O,与相交于点F.则=cm.
15. 把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6厘米,DC=7厘米.把三角板DCE绕点C顺时针旋转15°得到 , 如图(2),这时AB与相交于点O,与相交于点F.则=cm. 16. 如图,一组x轴正半轴上的点 , , …满足条件 , 抛物线的顶点 , , …依次是反比例函数图象上的点,第一条抛物线以为顶点且过点O和;第二条抛物线以为顶点且经过点和;…第n条抛物线以为顶点且经过点 , , 依次连结抛物线的顶点和与x轴的两个交点,形成、、…、 . 请写出所有满足三角形面积为整数的n的值 .
16. 如图,一组x轴正半轴上的点 , , …满足条件 , 抛物线的顶点 , , …依次是反比例函数图象上的点,第一条抛物线以为顶点且过点O和;第二条抛物线以为顶点且经过点和;…第n条抛物线以为顶点且经过点 , , 依次连结抛物线的顶点和与x轴的两个交点,形成、、…、 . 请写出所有满足三角形面积为整数的n的值 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、计算: .(2)、解方程:;18. 已知抛物线y=ax2-2ax-3+2a2 (a<0).(1)、求这条抛物线的对称轴;(2)、若该抛物线的顶点在x轴上,求抛物线的函数解析式;19. 如图,正方形网格中(每个小正方形边长是1,小正方形的顶点叫做格点),△ABC的顶点均在格点上,请在所给的平面直角坐标系中解答下列问题:

⑴作出△ABC绕点C逆时针旋转90°后的;
⑵作出关于原点O成中心对称的 .
20. 我区某中学就新冠疫情对青少年价值观产生的影响做了一个问卷调查,其中一项调查内容是:疫情期间出现的哪一个高频词汇最触动你的内心?A.生命,B.感恩,C.责任,D.奉献.每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请份根据统计图提供的信息,解答下列问题: (1)、本次调查中,一共调查了名同学;(2)、扇形统计图中 ▲ , 并补全条形统计图;(3)、从该校学生中随机抽取一个最关注热词“感恩”的学生的概率是多少.21. 如图,点A、P、B、C是上的四个点,且 .
(1)、本次调查中,一共调查了名同学;(2)、扇形统计图中 ▲ , 并补全条形统计图;(3)、从该校学生中随机抽取一个最关注热词“感恩”的学生的概率是多少.21. 如图,点A、P、B、C是上的四个点,且 . (1)、证明:是正三角形.(2)、若的半径是6,求正的边长.22. 我市某苗木种植基地尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元株的果苗,售后经过统计得到此果苗,单日销售量株与第天为整数满足关系式: , 销售单价元株与之间的函数关系为 .(1)、计算第几天该果苗单价为25元株?(2)、求该基地销售这种果苗30天里单日所获利润元关于天的函数关系式;(3)、“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”试问:基地负责人这次为“精准扶贫”捐赠多少钱?23. 如图,已知抛物线与x轴交于点, , , 与y轴交与点D.过点的直线AC与抛物线交与A,F两点.
(1)、证明:是正三角形.(2)、若的半径是6,求正的边长.22. 我市某苗木种植基地尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元株的果苗,售后经过统计得到此果苗,单日销售量株与第天为整数满足关系式: , 销售单价元株与之间的函数关系为 .(1)、计算第几天该果苗单价为25元株?(2)、求该基地销售这种果苗30天里单日所获利润元关于天的函数关系式;(3)、“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”试问:基地负责人这次为“精准扶贫”捐赠多少钱?23. 如图,已知抛物线与x轴交于点, , , 与y轴交与点D.过点的直线AC与抛物线交与A,F两点. (1)、求抛物线的解析式;(2)、点P为直线AF下方抛物线上一动点,过点P作y轴的平行线交AC于点Q,过点Р作x轴的平行线交y轴于点E,求的最大值及相应点Р的坐标;(3)、在(2)的条件下,将抛物线先向右平移2个单位,再向下平移1个单位,得到新抛物线 , 点M为对称轴上一点,点N为上一点,若以点D,P,M,N为顶点的四边形为平行四边形,写出所有符合条件的点M的坐标,并任选其中一个点M的坐标写出求解过程.24. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)、求抛物线的解析式;(2)、点P为直线AF下方抛物线上一动点,过点P作y轴的平行线交AC于点Q,过点Р作x轴的平行线交y轴于点E,求的最大值及相应点Р的坐标;(3)、在(2)的条件下,将抛物线先向右平移2个单位,再向下平移1个单位,得到新抛物线 , 点M为对称轴上一点,点N为上一点,若以点D,P,M,N为顶点的四边形为平行四边形,写出所有符合条件的点M的坐标,并任选其中一个点M的坐标写出求解过程.24. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°. (1)、将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)、将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.
(1)、将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)、将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.①在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;
②将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系(直接写出结果).