浙江省舟山市定海六中2022-2023学年九年级上学期9月月考数学试题卷

试卷更新日期：2022-10-11 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分.）

1. 将一元二次方程 $3 x^{2} - 1 = 5 x$ 化为一般形式后，其中二次项系数、一次项系数、常数项分别是（）

A、3，5，-1 B、-3，5，1 C、3，-5，-1 D、3，-5，13

查看试题解析
2. 如图，四个转盘分别被分成不同的等份．若让转盘自由转动一次，停止后指针落在阴影区域内的概率最大的转盘是（）

A、 B、 C、 D、

查看试题解析
3. 如果 $y = (m - 2) x^{2} + (m - 1) x$ 是关于x的二次函数，则m的取值范围是（）

A、 $m \neq 1$ B、 $m \neq 2$ C、 $m \neq 2$ 且 $m \neq 1$ D、全体实数

查看试题解析
4. 把如图的交通图案绕着它的中心旋转一定角度后与自身重合，则至少旋转（）

A、30° B、60° C、120° D、180°

查看试题解析
5. 如图，两条抛物线 $y_{1} = - \frac{1}{2} x^{2} + 1$ $， y_{2} = - \frac{1}{2} x^{2} - 1$ 与分别过点（ $- 2$ ， $- 1$ ）（2， $- 3$ ）且平行于 y 轴的两条平行线围成的阴部分的面积为（）

A、10 B、8 C、6 D、4

查看试题解析
6. 在一个不透明的口袋中，放置6个黄球、1个红球和n个蓝球，这些小球除颜色外其余均相同，课外兴趣小组每次摸出一个球记录下颜色后再放回，并且统计了黄球出现的频率，如图，则n的值是（）

A、2 B、3 C、5 D、8

查看试题解析
7. 如图，已知在 $⊙ O$ 中， $B C$ 是直径， $A B = D C$ ，则下列结论不一定成立的是（）

A、 $O A = O B = A B$ B、 $∠ A O B = ∠ C O D$ C、 $\overset{⌢}{A B} = \overset{⌢}{D C}$ D、 $O$ 到 $A B$ 、 $C D$ 的距离相等

查看试题解析
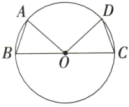8. 如图是拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y=-0.01（x-20）²+4，桥拱与桥墩AC的交点C恰好位于水面，且AC⊥x轴，若OA=5米，则桥面离水面的高度AC为（）

A、5米 B、4米 C、2.25米 D、1.25米

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，分别以AB，BC，CA为直径作半圆围成两月牙形，过点C作DF $//$ AB分别交三个半圆于点D，E，F.若 $\frac{C E}{D F} = \frac{3}{5}$ ，AC+BC＝15，则阴影部分的面积为（）

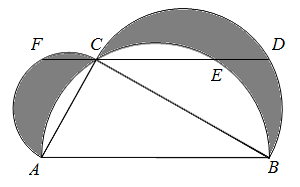A、16 B、20 C、25 D、30

查看试题解析
10. 如图，在平面直角坐标系中，点A，C，N的坐标分别为（-2，0），（2，0），（4，3），以点C为圆心，2为半径画⊙C，点P在⊙C上运动，连接AP，交⊙C于点Q，点M为线段QP的中点，连接MN，则线段MN的最小值为（）

A、 $\sqrt{21 - 6 \sqrt{3}}$ B、3 C、 $\sqrt{13}$ D、 $\sqrt{10}$

查看试题解析

二、填空题(本题有6小题,每小题4分,共24分)

11. 有五张背面完全相同的纸质卡片，其正面分别标有数：6、 $\frac{8 \sqrt{3}}{3} π$ 、 $- \sqrt[3]{64}$ 、 $\sqrt{16}$ －2、 $\frac{\sqrt{2}}{2}$ ．将它们背面朝上洗匀后，从中随机抽取一张卡片，则其正面的数是无理数的概率是．

查看试题解析
12. 已知A为⊙O外一点，若点A到⊙O上的点的最短距离为2，最长距离为4，则⊙O的半径为．

查看试题解析
13. 已知 $y = (m + 2) x^{m^{2} - 2}$ 是二次函数，则m= ．

查看试题解析
14. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象过点 $(- 2 ， 0) ， (x_{0} ， 0) ， 0 < x_{0} < 1$ ，与y轴正半轴相交，且交点在 $(0 ， 1)$ 的上方，下列结论：①2a﹣b＜0；②当x＞﹣1时，y随着x增大而减小；③ ${(a + c)}^{2} < b^{2}$ ；④ $b > 2 a + \frac{1}{2}$ ．其中一定成立的结论的序号是．

查看试题解析
15. “一切为了U”是常山在赶考共同富裕道路上，最新确定的城市品牌．已知线段 $A B$ ，对于坐标平面内的一个动点P，如果满足 $∠ A P B = 30 °$ ，则称点P为线段 $A B$ 的“U点”，如图，二次函数 $y = \frac{1}{2} x^{2} + 3 x + \frac{5}{2}$ 与x轴交于点A和点B．（1）线段 $A B$ 的长度为；（2）若线段 $A B$ 的“U”点落在y轴的正半轴上，则该“U点”的坐标为．

查看试题解析
16. 如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式 $y = a (x - 6)^{2} + h$ ．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．若球能越过球网，又不出边界，则h的取值范围为．

查看试题解析

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17.

(1)、解方程： $x^{2} + 4 x - 3 = 0$ ．

(2)、先化简，再求值： $(\frac{1}{n + 4} - 1) \div \frac{n^{2} - 9}{n^{2} + 8 n + 16}$ ，然后从 $- 4$ ， $- 3$ ， $0$ ， $3$ 中选择一个合适的整数代入求值．

查看试题解析
18. 已知函数y=（m²-2）x²+（m+ $\sqrt{2}$ ）x+8．

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，求m的取值范围.

查看试题解析
19. 利用对称性可以设计美丽的图案，在边长为1的正方形方格纸中，有如图所示的△ABC(顶点都在格点上)．

⑴先作出该三角形关于直线 $l$ 成轴对称的 $△ A^{'} B^{'} C^{'}$ ；

⑵再作将 $△ A^{'} B^{'} C^{'}$ 绕点 $B ′$ 顺时针方向旋转90°后的 $△ A ″ B^{'} C ″$ ；

⑶求 $△ A ″ B^{'} C ″$ 的面积．

查看试题解析
20. 为提升学生的艺术素养，学校计划开设四门艺术选性课：A.书法：B.绘画：C.乐器：D.舞蹈.为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）.将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：

(1)、本次调查的学生共有人；扇形统计图中∠α=度；

(2)、请把条形统计图补充完整；

(3)、学校为举办2021年度校园文化艺术节，决定从A.书法；B.绘画；C.乐器；D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式，请用列表法或树状图求出选中书法与乐器组合在一起的概率．

查看试题解析
21. 在⊙O中，弦AB⊥AC，且AB=AC=6．D是⊙O上一点（不在 $\overset{⌢}{B A C}$ 上），连接AD、BD、CD．

(1)、如图①，若AD经过圆心O，求BD、CD的长；

(2)、如图②，若∠BAD=2∠DAC，连接BC、OD，且BC是直径，求BD、CD的长．

查看试题解析
22. 一大型商场经营某种品牌商品，该商品的进价为每件6元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元件）（x为正整数）之间满足一次函数关系，表格记录的是某三周的有关数据：
x（元/件）
7
8
9
y（件）
8500
8000
7500

(1)、求y与x的函数关系式（不求自变量的取值范围）；

(2)、在销售过程中要求销售单价不低于成本价，且不高于17元/件，若某一周该商品的销售最不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？

(3)、抗疫期间，该商场这种商品售价不大于17元/件时，每销售一件商品便向某慈善机构捐赠m元（ $1 \leq m \leq 6$ ），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．

查看试题解析
23. 如图，抛物线 $C ： y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ，且抛物线经过 $M (1 ， 0) ， D (0 ， 3)$ 两点，与x轴交于点N．

(1)、点N的坐标为．

(2)、已知抛物线 $C_{1}$ 与抛物线C关于y轴对称，且抛物线 $C_{1}$ 与x轴交于点A， $B_{1}$ （点A在点 $B_{1}$ 的左边）．
①抛物线 $C_{1}$ 的解析式？

②当抛物线 $C_{1}$ 和抛物线C上y都随x的增大而增大时，请直接写出此时x的取值范围．

(3)、若抛物线 $C_{n}$ 的解析式为 $y = - (x + 1) (x - 2 - n) (n = 1 ， 2 ， 3 ⋯)$ ，抛物线 $C_{n}$ 的顶点为 $P_{n}$ ，与x轴的交点为A， $B_{n}$ （点A在，点 $B_{n}$ 的左边）．判断抛物线的顶，点 $P_{1} ， P_{2} ， P_{3} ， ⋯ ， P_{n}$ 是否在一条直线上，若在，请直接写出该直线的解析式；若不在，请说明理由．

查看试题解析
24. 定义：若两个三角形中，有两组边对应相等且其中一组等边所对的角对应相等，但不是全等三角形，我们就称这两个三角形为偏等三角形．

(1)、如图1，点 $C$ 是弧 $B D$ 的中点， $∠ D A B$ 是弧 $B D$ 所对的圆周角， $A D > A B ，$ 连接 $A C$ 、 $D C 、 C B ，$ 试说明 $△ A C B$ 与 $△ A C D$ 是偏等三角形．

(2)、如图2， $△ A B C$ 与 $△ D E F$ 是偏等三角形，其中 $∠ A = ∠ D ， A C = D F ， B C = E F ，$ 猜想结论：一对偏等三角形中，一组等边的对角相等，另一组等边的对角．请填写结论，并说明理由．(以 $△ A B C$ 与 $△ D E F$ 为例说明)；

(3)、如图3， $△ A B C$ 内接于 $⊙ O ， A C = 6 ， ∠ A = 30 ° ， ∠ C = 45 ° ，$ 若点 $D$ 在 $⊙ O$ 上，且 $△ A D C$ 与 $△ A B C$ 是偏等三角形， $A D > C D ，$ 求 $A D$ 的值．

查看试题解析

x（元/件）	7	8	9
y（件）	8500	8000	7500