人教版八上数学第十四章14.2.1平方差公式 课时易错题三刷(第二刷)
试卷更新日期:2022-10-10 类型:同步测试
一、单选题
-
1. 计算 ( )A、 B、 C、 D、
-
2. 下列多项式中能用平方差公式分解因式的是( )A、﹣a2﹣b2 B、x2+(﹣y)2 C、(﹣x)2+(﹣y)2 D、﹣m2+1
-
3. 记 则x+1=( )A、一个奇数 B、一个质数 C、一个整数的平方 D、一个整数的立方
-
4. ··· 的个位数是( )A、4 B、5 C、6 D、8
-
5. ,则a,b,c的大小关系正确的是( )A、a<b<c B、a<c<b C、b<a<c D、c<b<a
-
6. 已知a-b=2,则a2−b2-4b的值为( ).A、2 B、4 C、6 D、8
-
7. 若a,b,c是三角形的三边,则代数式(a-b)2-c2的值是( )A、正数 B、负数 C、等于零 D、不能确定
二、填空题
-
8. 如果(2a+2b+1)(2a+2b-1)=63,那么a+b的值为 .
-
9. 若实数满足(3x2+2y2+2019)(3x2+2y2﹣2019)=1﹣20192 , 则3x2+2y2的值为.
三、计算题
四、解答题
-
12. 学习了因式分解的知识后,老师提出了这样一个问题:设 为整数,则 的值一定能被20整除吗?若能,请说明理由?若不能,请举出一个反例,你能回答这个问题吗?
五、综合题
-
13. 如图,图1为边长为a的大正方形中有一个边长为b的小正方形,图2是由图1中阴影部分拼成的一个长方形.
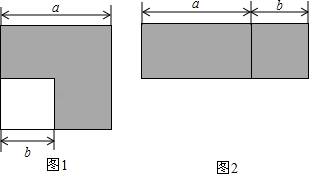 (1)、设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请用含a、b的代数式表示:S1= , S2=(只需表示,不必化简);(2)、以上结果可以验证哪个乘法公式?请写出这个乘法公式 ;(3)、运用(2)中得到的公式,计算:20152﹣2016×2014.
(1)、设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请用含a、b的代数式表示:S1= , S2=(只需表示,不必化简);(2)、以上结果可以验证哪个乘法公式?请写出这个乘法公式 ;(3)、运用(2)中得到的公式,计算:20152﹣2016×2014. -
14. 如图,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
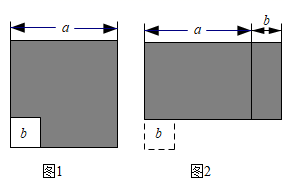 (1)、请问用这两个图可以验证公式法因式分解中的哪个公式?(直接写出公式)(2)、试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1.直接写出计算结果 .(3)、若图(1)中的阴影部分的面积是16,a﹣b=2,直接写出a4﹣b4的值.
(1)、请问用这两个图可以验证公式法因式分解中的哪个公式?(直接写出公式)(2)、试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1.直接写出计算结果 .(3)、若图(1)中的阴影部分的面积是16,a﹣b=2,直接写出a4﹣b4的值. -
15. 如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
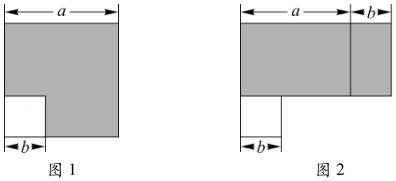 (1)、写出根据上述操作利用阴影部分的面积关系得到的等式:.(2)、请应用(1)中的等式,解答下列问题:
(1)、写出根据上述操作利用阴影部分的面积关系得到的等式:.(2)、请应用(1)中的等式,解答下列问题:①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
