河南省豫南名校2022-2023学年高三上学期理数9月质量检测试卷
试卷更新日期:2022-10-10 类型:月考试卷
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知命题 , . ( ).A、p为真命题, , B、p为假命题, , C、p为真命题, , D、p为假命题, ,3. 已知的垂心为M,则“M在的外部”是“钝角三角形”的( ).A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件4. 已知点在函数的图象上,且在第二象限内,若的图象在点处的切线斜率为1,则点的坐标为( )A、 B、 C、 D、5. 已知 , 则( )A、 B、 C、-3 D、36. 已知函数图象的一条对称轴为直线 , 则的最小值为( )A、2 B、3 C、4 D、57. 函数的大致图像为( )A、
 B、
B、 C、
C、 D、
D、 8. 古代文人墨客与丹青手都善于在纸扇上题字题画,题字题画的部分多为扇环.已知某扇形的扇环如图所示,其中外弧线的长为60cm,内弧线的长为20cm,连接外弧与内弧的两端的线段均为16cm,则该扇形的中心角的弧度数为( ).
8. 古代文人墨客与丹青手都善于在纸扇上题字题画,题字题画的部分多为扇环.已知某扇形的扇环如图所示,其中外弧线的长为60cm,内弧线的长为20cm,连接外弧与内弧的两端的线段均为16cm,则该扇形的中心角的弧度数为( ). A、2.3 B、2.5 C、2.4 D、2.69. 已知函数满足 , 函数与图象的交点分别为 , , , , , 则( )A、-10 B、-5 C、5 D、1010. “学如逆水行舟,不进则退;心似平原跑马,易放难收.”《增广贤文》是勉励人们专心学习的.如果每天的“进步”率都是1%,那么一年后是;如果每天的“退步”率都是1%,那么一年后是 , 一年后“进步”的是“退步”的倍.如果每天的“进步”率和“退步”率都是20%,那么“进步”的是“退步”的1000倍需要经过的时间大约是(参考数据:1g 2≈0.3010,lg 3≈0.4771)( )A、15天 B、17天 C、19天 D、21天11. 已知函数若关于的方程有4个不同的实根,则的取值范围是( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、
A、2.3 B、2.5 C、2.4 D、2.69. 已知函数满足 , 函数与图象的交点分别为 , , , , , 则( )A、-10 B、-5 C、5 D、1010. “学如逆水行舟,不进则退;心似平原跑马,易放难收.”《增广贤文》是勉励人们专心学习的.如果每天的“进步”率都是1%,那么一年后是;如果每天的“退步”率都是1%,那么一年后是 , 一年后“进步”的是“退步”的倍.如果每天的“进步”率和“退步”率都是20%,那么“进步”的是“退步”的1000倍需要经过的时间大约是(参考数据:1g 2≈0.3010,lg 3≈0.4771)( )A、15天 B、17天 C、19天 D、21天11. 已知函数若关于的方程有4个不同的实根,则的取值范围是( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、二、填空题
-
13. 设 , , 则 .14. 生物学家为了了解抗生素对生态环境的影响,常通过检测水中生物体内抗生素的残留量来进行判断.已知水中某生物体内抗生素的残留量(单位:)与时间(单位:年)近似满足关系式 , , 其中为抗生素的残留系数,当时, , 则 .15. 写出一个同时满足下列三个性质的函数: .
①定义域为;②;③的导函数 .
16. 在中,内角所对的边分别是 , 且 , 点是线段的中点,若 , 则面积的最大值是.三、解答题
-
17. 的内角的对边分别是.已知.(1)、求角;(2)、若 , 且的面积为 , 求的周长.18. 已知:“实数满足”,“都有意义”.(1)、已知为假命题,为真命题,求实数的取值范围;(2)、若是的充分不必要条件,求实数的取值范围.19. 已知函数的部分图象如图所示.
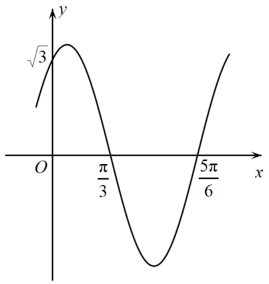 (1)、求的解析式;(2)、若函数 , 对任意的恒成立,求的取值范围.
(1)、求的解析式;(2)、若函数 , 对任意的恒成立,求的取值范围.