湖南省长沙二十一中2022-2023学年八年级上学期开学数学试卷
试卷更新日期：2022-10-09 类型：开学考试
一、单选题（3×12＝36）.
-
1. 下列各数中，属于无理数的是（ ）A、1.414 B、 C、 D、2. 下列调查中，适宜采用普查方式的是（ ）A、了解一批圆珠笔的寿命 B、了解全国七年级学生身高的现状 C、了解市民对“垃圾分类知识”的知晓程度 D、检查一枚用于发射卫星的运载火箭的各零部件3. 点P（﹣5，2）是第几象限内的点（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列长度的三条线段能组成三角形的是（ ）A、3，4，8 B、5，6，11 C、5，6，10 D、5，5，105.
如图，直线l与直线a、b相交，且ab，∠1＝80°， 则∠2的度数是（ ）
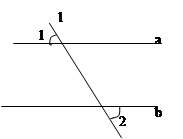
A、60° B、80° C、100° D、120°6. 如果一个多边形的每一个外角都是45°，那么这个多边形的内角和是（ ）A、540° B、720° C、1080° D、1260°7. 将点A（﹣2，3）沿x轴向左平移3个单位长度，再沿y轴向上平移4个单位长度后得到的点A′的坐标为（ ）A、（1，7） B、（1．﹣1） C、（﹣5，﹣1） D、（﹣5，7）8. 二元一次方程x+3y=10的非负整数解共有（ ）对．A、1 B、2 C、3 D、49. 估计的值在（ ）之间．A、1和2 B、2和3 C、3和4 D、4与510. 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架，其中《盈不足》卷记载了一道有趣的数学问题：“今有共买物，人出八，赢三；人出七，不足四，问人数、物价各几何？”译文：“今有人合伙购物，每人出8钱，会多出3钱；每人出7钱，又差4钱，问人数，物价各多少？”设人数为x人，物价为y钱，根据题意，下面所列方程组正确的是（ ）
A、 B、 C、 D、11. 若实数a，b，c在数轴上对应点的位置如图所示，则下列不等式成立的是（ ）
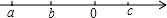A、ac＞bc B、a+c＞b+c C、ab＞cb D、a+b＞c+b12. 若不等式组无解，那么m的取值范围是（ ）A、m＞2 B、m＜2 C、m≥2 D、m≤2二、填空题（3×6＝18）
-
13. 的平方根是 ．14. 如图，在△ABC中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，∠A＝46°，∠1＝52°，则∠2＝度．
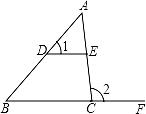15. 一个多边形的内角和等于1080°，它是边形．16. 点P在y轴的右侧，到x轴的距离是2，到y轴的距离是3，则P点的坐标是 ．17. 等腰三角形的两边长分别为 ，其周长为cm．18. 如图，D、E分别是△ABC边AB、BC上的点，AD＝2BD，BE＝CE，设△ADC的面积为S1 ， △ACE的面积为S2 ， 若S△ABC＝12，则S1+S2＝ ．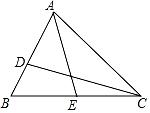
三、计算题（6×4＝24）
-
19. 计算：（﹣1）3+|1﹣ |+ ．20. 解方程组：21. 解不等式：2（x﹣1）+4＞0．22. 解不等式组
四、解答题
-
23. 湖南广益实验中学在暑假期间开展“心怀感恩，孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务，开学以后，校学生会随机抽取了部分学生，就暑假“平均每天帮助父母干家务所用时长”进行了调查，如图是根据相关数据绘制的统计图的一部分．
根据上述信息，回答下列问题：
(1)、在本次随机抽取的样本中，调查的学生人数是 人，m＝ ， n＝；(2)、补全数分布直方图；(3)、如果该校共有学生4000人，请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有多少人？24. 如图，AD为△ABC的中线，BE为△ABD的中线，过点E作EF垂直BC，垂足为点F．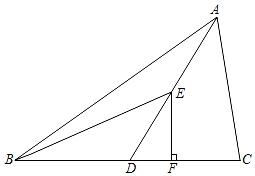
(1)、∠ABC＝35°，∠EBD＝18°，∠BAD＝30°，求∠BED的度数；(2)、若△ABC的面积为30，EF＝5，求CD的长度．25. 在国家精准扶贫政策下，某乡村大力发展乡村旅游，为了满足游客的需求，某商户决定购进A，B两种特产来进行销售．(1)、若购进A种特产8件，B种特产3件，需要950元；购进A种特产5件，B种特产6件，需要800元．求购进A，B两种特产每件分别需要多少元？(2)、若该商户决定购进A，B两种特产共100件，考虑市场需求和资金周转，A种特产至少需购进50件，用于购买这100件特产的总资金不能超过7650元，请问该商户最多可购进A种特产多少件？
